Структура этого пространства основана на работах по организации системы визуального восприятия на трех оппозициях:
· черный — белый (ахроматическая ось);
· красный — зеленый;
· желтый — синий;
(См. § 3.6.)
Центром этого пространства является ахроматическая ось. Оно вычисляется для каждого стандартного источника света.
На оси + а* – а* красный находится в оппозиции с зеленым.
На оси + b* – b* желтый находится в оппозиции с синим.
Ось L* обозначает светлоту (luma) во избежание смешения этого термина с понятием яркости в фотометрии.
В таком пространстве эллипсы равного восприятия должны иметь равную площадь.
Радиус круга с площадью, равной площади эллипсов, четко определяет единицу для каждого из трех измерений.
Переход от пространства МКО ХУZ к пространству L*, а*, b* возможен, но преобразования в этом случае будут нелинейными.
Пусть ![]() —
трихроматические координаты эталонного белого, взятого в качестве идеального рассеивателя.
—
трихроматические координаты эталонного белого, взятого в качестве идеального рассеивателя.
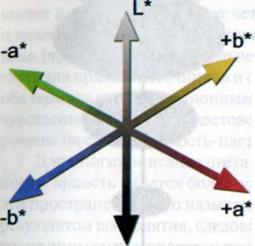
Рис. 5.23. Три оси пространства МКО LAB
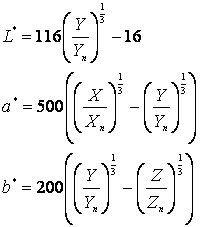
Если ![]() > 0,008856,
то:
> 0,008856,
то:
 ,
,
иначе:
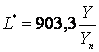

при ![]() (значение) = значение
(значение) = значение ![]() ,
если значение > 0,008856,
,
если значение > 0,008856,
иначе ![]() (значение) = 7,787значение +
(значение) = 7,787значение + ![]() .
.
Отметим, что условия, выдвинутые Паули:

предполагают, что эталонные цветовые компоненты достаточно удалены от белой точки. С другой стороны, значение яркости V соответствует ее значению на кривой чувствительности глаза к яркости, определение которой было дано выше (см. §3.8).
Если условия Паули учитываются, то уравнения можно записать в упрощенном виде:
С помощью обратной операции можно перейти от системы МКО LAB к системе МКО XYZ.
Если ![]() ,
то
,
то 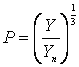
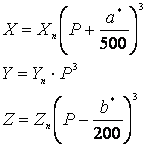
Система LAB позволяет использование цилиндрических координат пространства TSL с координатами L*, С*, Н*. Н* – это цветовой тон (hue), С* – уровень насыщенности (chroma), а значение светлоты (luma) остается постоянным.
L* = L*
Н*![]() =
=
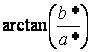 при a
≠ 0
при a
≠ 0
![]()
Для всех случаев полное отклонение цвета ![]()
![]() ,
,
а отклонение цветового тона:
![]()
Чтобы глаз смог заметить разницу между
цветами, необходимо отклонение хотя бы в единицу, ![]() = 1,
однако на практике часто допускаются и колориметрические отклонения
= 1,
однако на практике часто допускаются и колориметрические отклонения ![]() = 5.
= 5.
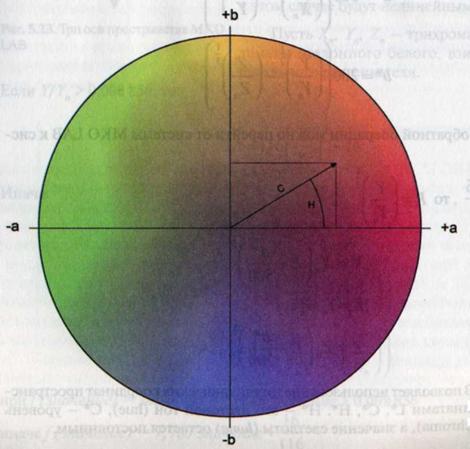
Рис. 5.24. Цветовой круг в пространстве МКО L*a*b*
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.