1. Существует множество систем RGB, зависящих от цветовой базы системы.
2. Очень трудно сравнивать разные системы и осуществлять переход от одной системы к другой.
3. Координаты RGB и трихроматические компоненты могут принимать отрицательные значения.
4. Значения трихроматических компонентов условны. Они связаны с яркостью. Яркость трихроматических компонентов является линейной величиной, в отличие от самих компонентов.
В 1931 году работы Джадда позволили МКО разработать эталонную колориметрическую систему, в которой основные цветовые компоненты являются виртуальными, то есть не существуют в реальности. Система МКО XYZ отображает изменение основных цветов и является результатом матрицы преобразования системы RGB.

Матрица преобразования — это общая математическая операция, осуществляющая линейное преобразование пространства, то есть после такого преобразования треугольник видоизменится по отношению к исходному, но ни в коем случае не фигура, состоящая из кривых.
Матрицы - это довольно простые операции, но они требуют точности в выполнении. Операции предыдущего преобразования можно записать и таким образом:

В свое время матрицы преобразования пространства RGB в XYZ записывались так:
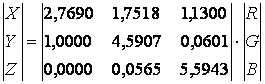
Составляющая Y(λ) эквивалентна функции относительной яркости, G(λ), что позволяет представить яркость как Y. Чтобы достичь этого, необходимо разделить все коэффициенты на значение яркости белой точки так, чтобы сумма всех факторов, определяющих Y, равнялась 1. Поэтому матрицы преобразования пространства RGB в XYZ МКО были представлены в следующем виде:
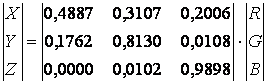
Можно проверить, что значение Y равно единице:
0,1762 + 0,8130 + 0,0108 = 1
Следующая операция позволяет перейти к двухмерному пространству МКО ХYZ:
сумма = X + У + Z
Если сумма ≠ 0, тогда:
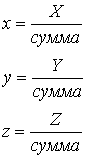
Следовательно, ![]()
В такой системе все координаты имеют положительные значения, а х, у, z больше нуля и меньше единицы. Их сумма равна единице. Необходимо различать, с одной стороны, координаты X, У, Z (пpoпиcныe буквы) и, с другой стороны, х, у, z (строчные). Значение z можно вывести, исходя из значений х и у:
z = 1-(х + у)
Это пространство можно представить как пространство с двумя измерениями х, у, к которым добавляется значение яркости Y. Это пространство называется пространством МКО хуY.
Полученная кривая — это линия спектральных цветов, то есть линия длин волны спектра видимого света от 380 нм до 770 нм, причем на пределах спектра она сильно сжата. Линия, соединяющая два противоположных предела спектра, называется линией пурпурных цветов. Это область неспектральных цветов, потому что пурпурный цвет обладает не одной, а двумя доминантными длинами волны. Напомним, что из-за этого физики называют пурпурный цвет minus green.
• Расчет спектральных цветов и чистоты цвета
Чтобы получить значение доминирующей длины волны данного цвета (у пурпурных цветов оно будет отрицательным) в этом пространстве, достаточно провести линию, проходящую через белую точку и рассматриваемый цвет.
Можно также, при условии симметрии вокруг белой точки, вычислить дополнительный цвет данного цвета.
Доминирующая длина волны неспектральных
(пурпурных) цветов обозначается — ![]() и равна длине
волны дополнительного цвета.
и равна длине
волны дополнительного цвета.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.