В практических приложениях имеет большое значение задача о нахождении кратчайшего пути между двумя вершинами связанного графа.
Задача о кратчайшем пути на графе в общем виде может быть сформулирована следующем образом.
Дан граф ![]() . Каждому ребру
этого графа приписано некоторое число
. Каждому ребру
этого графа приписано некоторое число ![]() ,
называемое длиной ребра. В частных случаях
,
называемое длиной ребра. В частных случаях ![]() может
быть расстоянием между вершинами, соединяемыми ребром u,
временем или стоимостью проезда по этому ребру и т.п. При этом любая цепь
может
быть расстоянием между вершинами, соединяемыми ребром u,
временем или стоимостью проезда по этому ребру и т.п. При этом любая цепь ![]() будет характеризоваться длиной
будет характеризоваться длиной
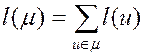 (2.1)
(2.1)
Требуется для двух произвольных вершин а и b
графа Gнайти
путь ![]() , причем такой, чтобы его полная длина
была наименьшей [13].
, причем такой, чтобы его полная длина
была наименьшей [13].
Сначала рассмотрим правило для решения задачи частного вида, когда длина каждого ребра равна 1.
Общее правило для нахождения кратчайшего пути в графе
состоит в том, чтобы каждой вершине ![]() приписать индекс
приписать индекс ![]() , равный длине кратчайшего пути из данной
вершины в конечную вершину [13].
, равный длине кратчайшего пути из данной
вершины в конечную вершину [13].
Приписывание индексов в случае графа с ребрами единичной длины производится в следующем порядке.
1.
Конечной вершине ![]() приписывается индекс 0.
приписывается индекс 0.
2. Всем вершинам, из которых идет ребро в конечную вершину, приписывается индекс 1.
3.
Всем вершинам, еще не имеющим
индексов, из которых идет ребро в вершину с индексом ![]() ,
приписывается индекс
,
приписывается индекс ![]() .
.
Этот процесс продолжается до тех пор, пока не будет помечена начальная вершина. По окончании разметки индекс у начальной вершины будет равен длине кратчайшего пути. Сам кратчайший путь найдем, если будем двигаться из начальной вершины в направлении убывания индексов.
Задача приписывания вершинам графа числовых индексов усложняется, если ребра графа имеют произвольную длину.
Процесс приписывания индексов для такого графа заключается в следующем [13].
1.
Каждая вершина ![]() помечается индексом
помечается индексом ![]() . Первоначально конечной вершине
. Первоначально конечной вершине ![]() приписывается индекс
приписывается индекс ![]() . Для остальных вершин предварительно
полагаем
. Для остальных вершин предварительно
полагаем ![]() .
.
2.
Ищем такую дугу ![]() , для которой
, для которой ![]() , и
заменяем индекс
, и
заменяем индекс ![]() индексом
индексом ![]() .
.
Продолжаем этот процесс замены до тех пор, пока
остается хотя бы одна дуга, для которой можно уменьшить ![]() .
.
Сформулируем правило для нахождения кратчайшего пути.
Пусть ![]() – начальная вершина с
индексом
– начальная вершина с
индексом ![]() . Ищем вершину
. Ищем вершину ![]() такую,
что
такую,
что ![]() , и т.д. до тех пор, пока не дойдем до
конечной вершины
, и т.д. до тех пор, пока не дойдем до
конечной вершины ![]() . Путь
. Путь ![]() ,
длина которого равна
,
длина которого равна ![]() , является кратчайшим.
, является кратчайшим.
На рис. 2.12 представлен пример нахождения кратчайшего пути из вершины a в вершину b.
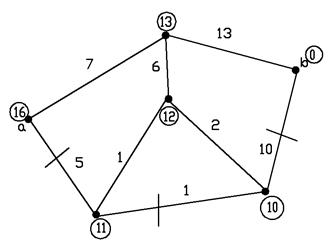
Рис. 2.12 Нахождение кратчайшего пути
Алгоритм нахождения длиннейшего пути представляет собой процесс приписывания индексов для вершин графа и заключается в следующем [15].
1
Каждая вершина ![]() помечается индексом
помечается индексом ![]() . Первоначально начальной вершине
. Первоначально начальной вершине ![]() приписывается индекс
приписывается индекс ![]() . Для остальных вершин предварительно
полагаем
. Для остальных вершин предварительно
полагаем ![]() .
.
2
Ищем такую дугу ![]() , для которой
, для которой ![]() , и
заменяем индекс
, и
заменяем индекс ![]() индексом
индексом ![]() .
.
Продолжаем
этот процесс замены до тех пор, пока остается хотя бы одна дуга, для которой
можно увеличить ![]() .
.
Пусть ![]() – конечная вершина с индексом
– конечная вершина с индексом ![]() . Ищем вершину
. Ищем вершину ![]() , такую,
что
, такую,
что ![]() , и т.д. до тех пор, пока не дойдем до начальной
вершины
, и т.д. до тех пор, пока не дойдем до начальной
вершины ![]() . Путь
. Путь ![]() , длина
которого равна
, длина
которого равна ![]() , является длиннейшим.
, является длиннейшим.
2.2.5 Алгоритм поиска тончайшего пути
Тончайшим путем между двумя вершинами графа называется путь минимальной тонкости.
1.
Начачальной вершине ![]() присваиваем метку
присваиваем метку ![]() , остальным вершинам
, остальным вершинам ![]() – метку
– метку ![]() .
Начальную вершину окрашиваем.
.
Начальную вершину окрашиваем.
2.
Для каждой неокрашенной вершины ![]() ,
связанной с последней окрашенной вершиной
,
связанной с последней окрашенной вершиной ![]() дугой
дугой ![]() пересчитываем ее метку по формуле
пересчитываем ее метку по формуле ![]() .
.
3.
Среди неокрашенных находим вершину ![]() с
минимальной меткой и окрашиваем ее и ведующую в нее из одной из ранее
окрашенных вершин
с
минимальной меткой и окрашиваем ее и ведующую в нее из одной из ранее
окрашенных вершин ![]() дугу
дугу ![]() ,
удовлетворяющую условию
,
удовлетворяющую условию ![]() . Если при этом
окрашенной оказалась конечная вершина, то задача решена, тонкость искомого пути
равна метке конечной вершины, а сам путь изображен на окрашенном дереве. В
противном случае переходим к п. 2.
. Если при этом
окрашенной оказалась конечная вершина, то задача решена, тонкость искомого пути
равна метке конечной вершины, а сам путь изображен на окрашенном дереве. В
противном случае переходим к п. 2.
По
окончании выполнения алгоритма окрашенные вершины и дуги составят корневое
дерево с корнем ![]() , отображающее тончайшие пути из
этой вершины во все остальные.
, отображающее тончайшие пути из
этой вершины во все остальные.
Технологической операцией будем называть последовательность переходов, выполняемых одним станком. При формировании технологических операций такого типа возникает следующая задача [22].
Дана
последовательность переходов ![]() в обработке
некоторой детали. Для каждого перехода заданы варианты выбора станков
в обработке
некоторой детали. Для каждого перехода заданы варианты выбора станков ![]() , которые могут его выполнить. Требуется
так выбрать станки для выполнения переходов, чтобы число получаемых при этом
операций было минимально. На рис. 2.13 приведены пример этой задачи и одно из
его решений. Покажем сводимость к задаче КРАТЧАЙШИЙ ПУТЬ.
, которые могут его выполнить. Требуется
так выбрать станки для выполнения переходов, чтобы число получаемых при этом
операций было минимально. На рис. 2.13 приведены пример этой задачи и одно из
его решений. Покажем сводимость к задаче КРАТЧАЙШИЙ ПУТЬ.
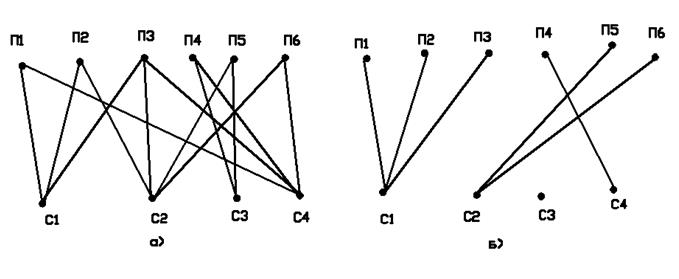
Рис. 2.13 Пример задачи формирования технологических операций а) и одного его решения б)
Построим
орграф с вершинами s, tи вершинами ![]() для
каждого перехода
для
каждого перехода ![]() и каждого станка
и каждого станка ![]() , который может его выполнить. Множество
дуг будут составлять дуги
, который может его выполнить. Множество
дуг будут составлять дуги ![]() , которые следует
провести для всех допустимых наборов значений индексов i, j, k. Все дуги
вида
, которые следует
провести для всех допустимых наборов значений индексов i, j, k. Все дуги
вида ![]() нагрузим нулем, остальные – единицей. На рис. 2.14
приведен пример построения орграфа для примера задачи (см. рис. 2.13).
нагрузим нулем, остальные – единицей. На рис. 2.14
приведен пример построения орграфа для примера задачи (см. рис. 2.13).
Произвольный путь из истока s в сток tна построенном взвешенном орграфе обладает следующими свойствами:
а)
промежуточные вершины пути ![]() определяют разбиение
последовательности переходов на операции, поскольку,
определяют разбиение
последовательности переходов на операции, поскольку, ![]() это
номера станков, которые их выполняют. Причем нет никакого варианта разбиения, которому
не соответствовал бы некоторый путь из sв t;
это
номера станков, которые их выполняют. Причем нет никакого варианта разбиения, которому
не соответствовал бы некоторый путь из sв t;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.