Практические приложения теории графов в машиностроении, страница 4

Без ограничения общности можно считать, что коэффициенты уравнения (2.2) различны. Если же найдутся такие и и v, что , то переменную   можно приравнять нулю, поскольку предметы типа vимеют тот же объем и не меньшую стоимость, чем предметы типа и. Находя все пары и и vс указанным свойством и устраняя переменные , можно добиться того, что коэффициенты при оставшихся переменных будут различны. Полученную таким образом задачу будем называть приведенной.

Ясно, что решение исходной задачи получается из решения приведенной приравниванием нулю устраненных переменных. Для сводимости необходима именно приведенная задача.

Построим орграф с вершинами  0, 1, 2, …, b. Дугу   проведем всякий раз, когда среди индексов коэффициентов 1, 2, ... ..., п, найдется такой индекс j, что . Поскольку коэффициенты  различны, для каждой дуги существует единственный такой индекс. Это позволяет нагрузить дуги  числами .

Рассмотрим пример построения орграфа для задачи:

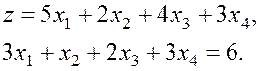                         (2.3)

В ограничении коэффициенты при  одинаковы. Устраняя , получаем приведенную задачу:

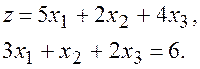                                        (2.4)

Орграф, соответствующий этой задаче, изображен на рис. 2.18.

Решение задачи  находится  следующим  образом. Для каждого  j=1, 2, ,..., п нужно просмотреть данный путь, найти все дуги  со свойством и посчитать их число. Оно – то и равно .

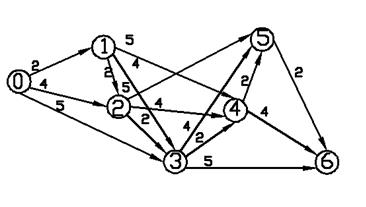
Рис. 2.18  Орграф для задачи (2.4)

На рис. 2.19 длиннейший путь выделен штрих-линией. Ему соответствует решение задачи (2.4): .

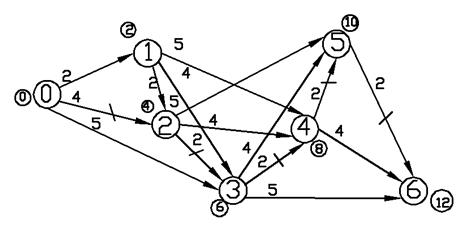
Рис. 2.19 Вариант решения 1 для задачи (2.4)

На рис. 2.20 длиннейший путь выделен штрих-линией. Ему соответствует решение задачи (2.4): .

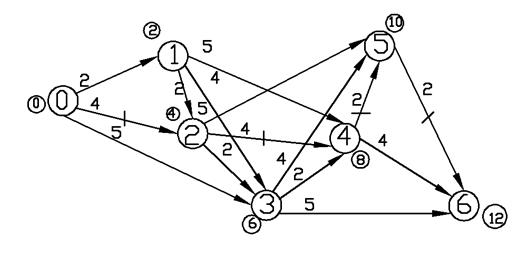
Рис. 2.20 Вариант решения 2 для задачи (2.4)

На рис. 2.21 длиннейший путь выделен штрих-линией. Ему соответствует решение задачи (2.4): .

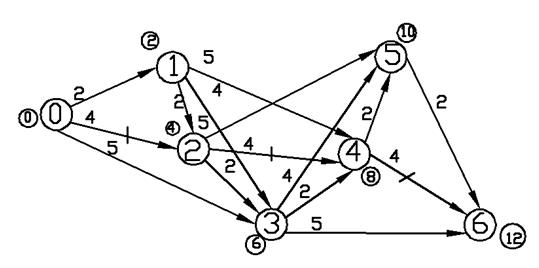
Рис. 2.21 Вариант решения 3 для задачи (2.4)

На рис. 2.22 длиннейший путь выделен штрих-линией. Ему соответствует решение задачи (2.4): .

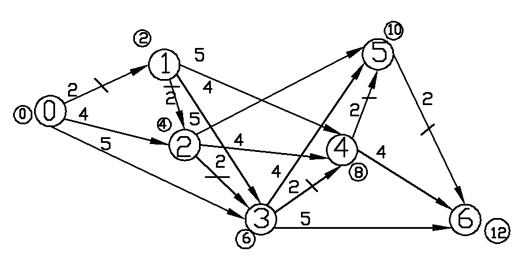
Рис. 2.22 Вариант решения 4 для задачи (2.4)

Аналогичная рюкзачная задача, в которой нужно минимизировать z, сводится к задаче КРАТЧАЙШИЙ ПУТЬ. При сводимости нужно лишь изменить правило построения приведенной задачи, устраняя вместо переменную .

В ограничении (2.3) коэффициенты при  одинаковы. Устраняя , получаем приведенную задачу:

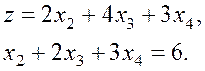                               (2.5)

На рис. 2.23 представлен орграф для задачи (2.5).

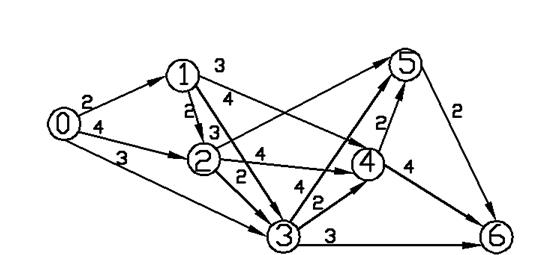
Рис. 2.23 Орграф для задачи (2.5)

Для задачи (2.5) есть только один кратчайший путь, проходящий через вершины 0, 3, 6. Ему соответствует решение задачи (2.5):  (см. рис. 2.24).

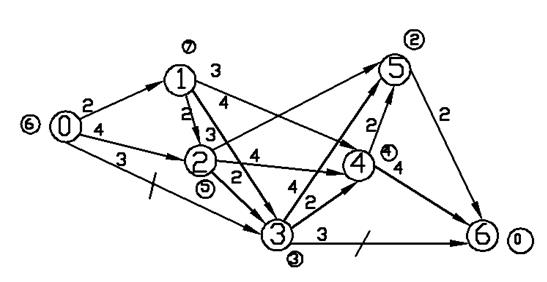
Рис. 2.24 Вариант решения 1 для задачи (2.5)

Вопросы для самопроверки

1.  Дайте два теоретико-множественных определений графа.

2.  Что такое    гамильтонов контур, путь?

3.  Что такое ребро, цепь, цикл, дерево?

4.  Какие матричные способы задания графа вы знаите?

5.  Что понимают под упорядочением вершин связного орграфа без контуров?

6.  Чем отличается упорядочивание вершин алгоритмом Фалкерсона от матричного способа упорядочивания?

7.  Задача о кратчайшемпути.

8.  Алгоритм поиска кратчайшего пути в орграфе

9.  Алгоритм поиска длиннейшегопути в орграфе.

10.  Алгоритм поиска тончайшегопути в орграфе.

11.  Правило построения орграфа для задачи «Формирование технологических операций».

12.  Как определить  количество операций с помощью орграфа в задаче «Формирование технологических операций»?

13.  Правило построения орграфа для задачи «Балансировка технологического маршрута».

14.  Сформулируйте задачу «Оснащение обрабатывающего центра»

15.  Правило построения орграфа для задачи «Оснащение обрабатывающего центра».