Практические приложения теории графов в машиностроении, страница 3

                           Таблица 2.9                              Таблица 2.10

Существуют следующие две модификации задачи балансировки. В первой требуется найти самый производительный, а не сбалансированный маршрут. Самым производительным является маршрут, который деталь проходит за минимальное время. Такая задача, очевидно, сводится к задаче КРАТЧАЙШИЙ ПУТЬ. Во второй модификации задано не время выполнения операций и транспортировки, а их скорость. Такая задача сводится к исходной заменой всех скоростных параметров Р на временные1/P. Однако можно поступить иначе. Сбалансированным можно считать маршрут, вдоль которого деталь проходит с наибольшей скоростью. Эта скорость будет определяться самым непроизводительным станком или самым низкоскоростным транспортным средством на маршруте. Им будет соответствовать самая короткая дуга на широчайшем пути из s в t, если все нулевые длины дуг в указанном взвешенном орграфе заменить на очень большие (превышающие практически возможные). Отсюда вытекает сводимость второй модификации к задаче ШИРОЧАЙШИЙ ПУТЬ.

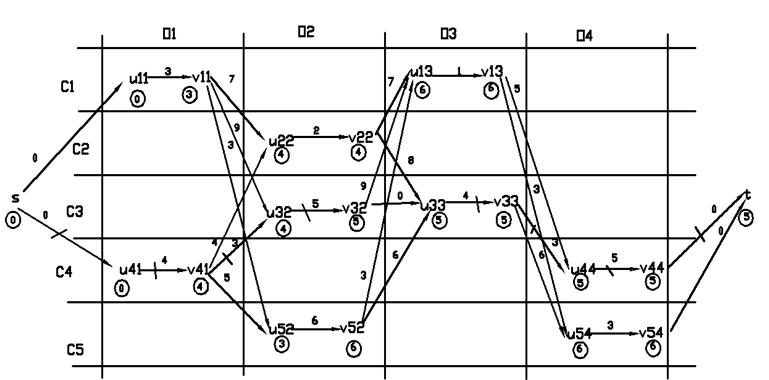
Рис. 2.16 Орграф для задачи балансировки с исходными данными на рис.2.15 и табл. 2.9, табл. 2.10

Под вершинами указана тонкость тончайшего пути, ведущего к ним из s; шрих-линией отмечен тончайший путь из s  в t с тонкостью 5.

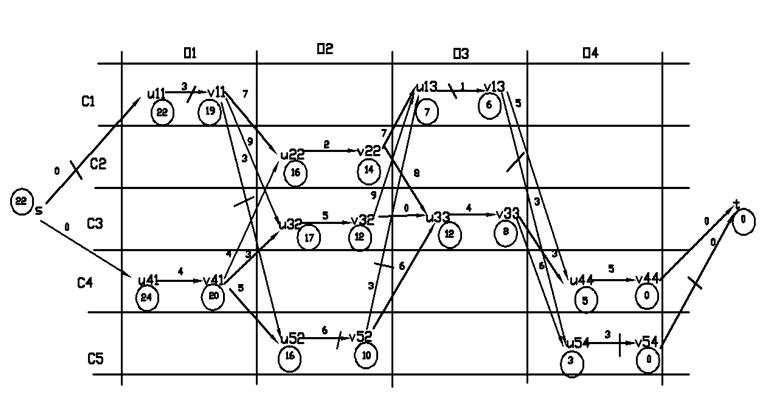Рис. 2.17 Орграф для задачи самый Производительный маршрут с исходными данными на рис.2.15 и табл. 2.9, 2.10

Минимальное время, за которое деталь проходит маршрут, равно 22 –  (см. рис. 2.17).

2.2.8 Оснащение обрабатывающего центра

Пусть имеется станок типа «обрабатывающий центр», магазин которого может оснащаться инструментами различных типов. Для инструмента каждого типа известно, сколько гнезд он занимает в магазине и каково время его работы. В магазине станка можно размещать несколько экземпляров инструмента одного типа. Требуется так оснастить станок инструментами, чтобы общее время их последовательной работы было максимальным, а емкость магазина была использована полностью [22].

Математическим описанием этой задачи является следующая задача рюкзачного типа.

ЦЕЛОЧИСЛЕННЫЙ РЮКЗАК С ОГРАНИЧЕНИЕМ –РАВЕНСТВОМ. Для положительных целых чисел  и неотрицательных вещественных чисел  найти неотрицательные целые значения переменных  , максимизирующие целевую функцию

при ограничении

                                           (2.2)

Параметр bможно рассматривать как объем рюкзака, в который можно укладывать предметы n типов, причем  по нескольку экземпляров каждого типа, а параметры   – как объем и стоимость одного предмета j-го типа. Равенство  означает, что в рюкзак укладывается kэкземпляров предмета j-го типа. Рюкзак нужно упаковать предметами так, чтобы его объем был использован полностью, а стоимость – максимальной. Объем рюкзака можно интерпретировать как объем магазина обрабатывающего центра, предметы – как инструменты с временем работы  и числами занимаемых гнезд  соответственно. Сформулированная рюкзачная задача сводится к задаче ДЛИННЕЙШИЙ ПУТЬ.