Практические приложения теории графов в машиностроении, страница 2

б) каждый набор промежуточных  вершин, лежащих  вдоль неудлиняемых участков пути с нулевой длиной, определяет одну операцию. Такими наборами в приведенном примере будут ;

в) каждая промежуточная дуга с единичной длиной определяет смену станка. Следовательно, длина пути без единицы равна числу операций.

Из этих свойств вытекает сводимость, поскольку по кратчайшему пути из истока в  сток на построенном взвешенном орграфе однозначно находится разбиение последовательности переходов на минимальное число операций [22].

На рис. 2.14 горизонтальные дуги нагружены нулем, остальные – единицей; жирные дуги обозначают кратчайший путь, соответствующий решению (б) на рис. 2.13; длина  пути без единицы равна числу операций, т е. трем операциям:

·  операция  включает переходы  и выполняется на станке ;

·  операция  включает переход  и выполняется на станке ;

·  операция  включает переходы   и выполняется на станке .

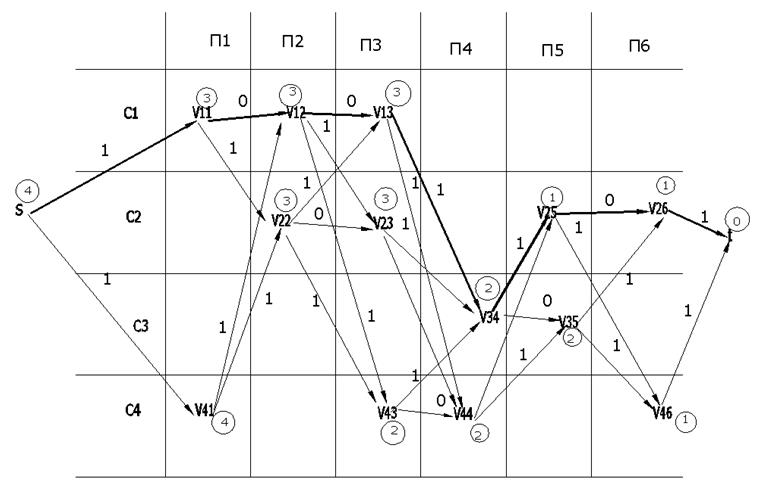
Рис. 2.14 Пример формирования технологических операций как поиска Кратчайшего Пути на орграфе

2.2.7 Балансировка технологического маршрута

Следующая производственная задача, сводимая к задаче поиска пути на графе, возникает при выборе технологических маршрутов обработки деталей в гибкой производственной системе (ГПС).

Пусть на вход некоторой ГПС поступила партия одинаковых деталей для изготовления изделий одной номенклатуры. Задана  установленная для этой номенклатуры последовательность технологических операций. Для каждой операции определены допустимые назначения на станки ГПС и время ее выполнения каждым подходящим станком. Время выполнения операции может зависеть от станка, который ее выполняет. Известно время транспортировки детали от одного станка к другому. Требуется так назначить операции на станки, чтобы получаемый при этом технологический маршрут прохождения станков был сбалансирован (т. е. длительности обработки и транспортировки детали на всех участках маршрута, по возможности, выравнены). Балансировка технологического маршрута приводит к наиболее равномерной загрузке оборудования ГПС [22].

Пусть  – последовательность  операций, а  – станки ГПС. Построим орграф с вершинами s, tи вершинами   для каждой операции  и каждого станка  , который может ее выполнить. Вершины соединим дугами  для всех допустимых наборов значений i, j, k.

Все дуги вида  нагрузим временем выполнения операции  станком , все дуги вида , – временем транспортировки от станка ; к станку , а все дуги вида – нулем.

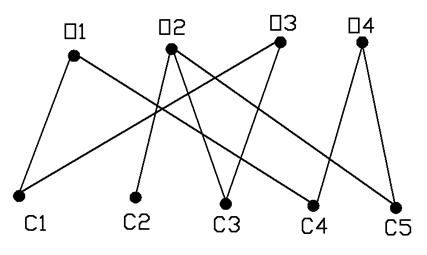
Рис. 2.15 Пример допустимых назначений операций на станки

Рассмотрим пример построения орграфа при п=4, т=5. Допустимые назначения операций на станки определены ребрами двудольного графа на рис. 2.15,  а время выполнения операций подходящими станками и время транспортировки представлены в таблицах 2.9 и 2.10. Клетки, соответствующие недопустимым назначениям операции на станки, не заполнены. На рис. 2.16 изображен соответствующий орграф.

Произвольный путь на построенном орграфе из s в tпроходит через промежуточные вершины   и обладает следующими свойствами:

а) он определяет вариант допустимого назначения операций на станки, поскольку  – это номера станков, которые должны выполнять операции . Причем нет ни одного варианта допустимого назначения операций, которому не соответствовал бы некоторый путь из sв t.

б) соответствующий путь маршрут проходит станки в последовательности  . Самая длинная дуга пути определяет самый длительный по времени процесс на маршруте. Если такой дугой окажется , то самым длительным процессом будет операция , если  то – транспортировка от станка к станку

Сбалансированному маршруту поставим в соответствие путь из s в tс наиболее короткой длиннейшей дугой. Тем самым время наиболее длительного процесса на маршруте мы сделаем по возможности меньше и приблизим его к времени остальных. Такая интерпретация критерия балансировки окончательно сводит исходную задачу к задаче ТОНЧАЙШИЙ ПУТЬ [22].