Тема 1. Предмет и метод финансовой математики
1.1 Определение предмета финансовой математики.
1.2 Время как фактор стоимости.
1.3 Сущность и виды процентных ставок.
1.4 Сущность базовых финансовых операций: наращение и дисконтирование.
1.5 Основные методы анализа финансовых потоков.
1.6 Производные модели финансовых расчетов.
Иллюстративный материал к теме
Предмет финансовой математики – количественный финансовый анализ экономических явлений и процессов.
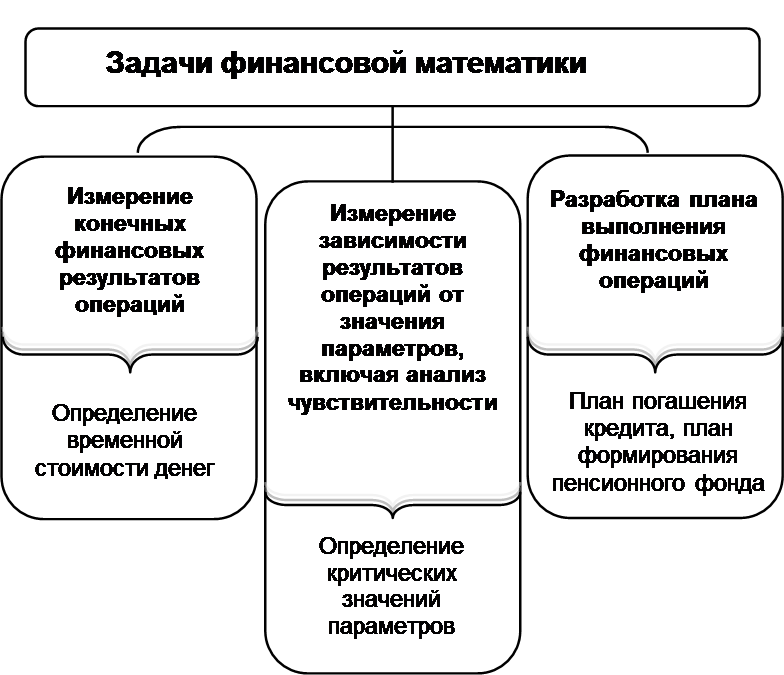
Рисунок 1.1 Задачи финансовой математики
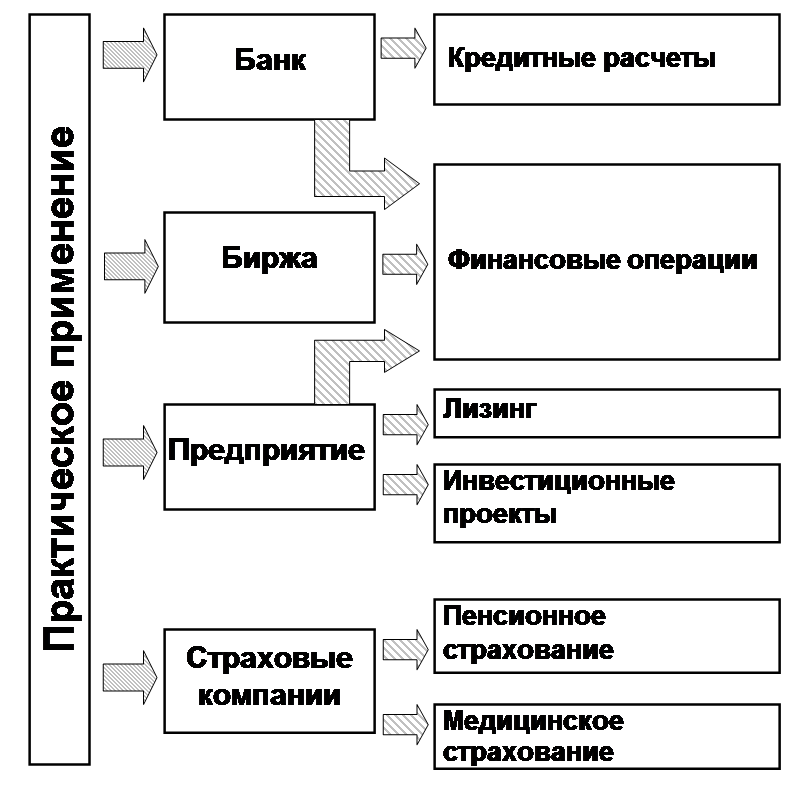
Рисунок 1.2 Практическое применение финансовой математики
Временная стоимость денег (time-valueofmoney) – зависимость стоимости денег от момента времени, в который они рассматриваются.
Причина: существование альтернативных издержек использования денег, которые прямопропорциональны времени, на которые отсрочено получение денег.
В качестве меры временной стоимости денег используется ставка процента. Под процентом (interest) (процентные деньги) понимают доход, получаемый владельце денег от предоставления их в долг в любой форме.
Процентная ставка (i) – это доля базовой суммы, подлежащая к уплате в виде процентов за определенный период, который называется периодом начисления.
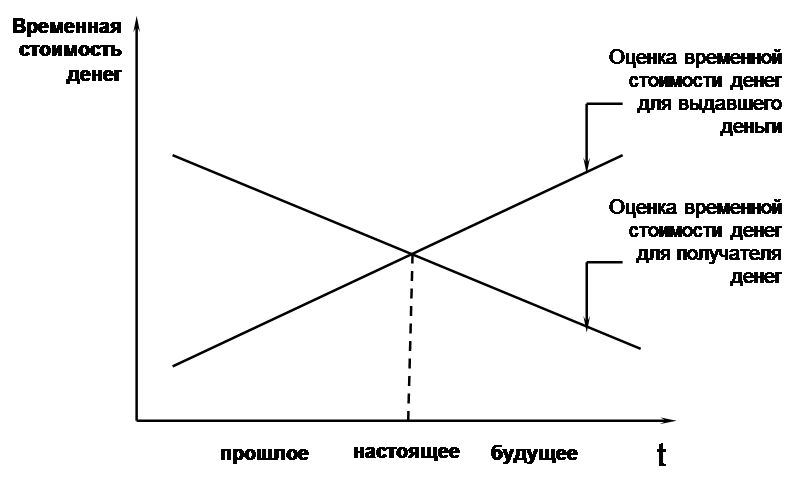
Рисунок 1.3 Временная стоимость денег
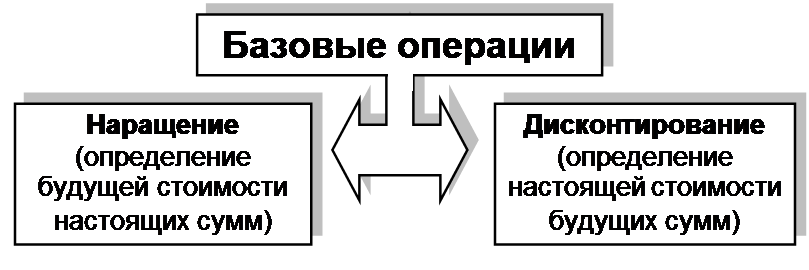
Рисунок 1.4 Сущность базовых финансовых операций
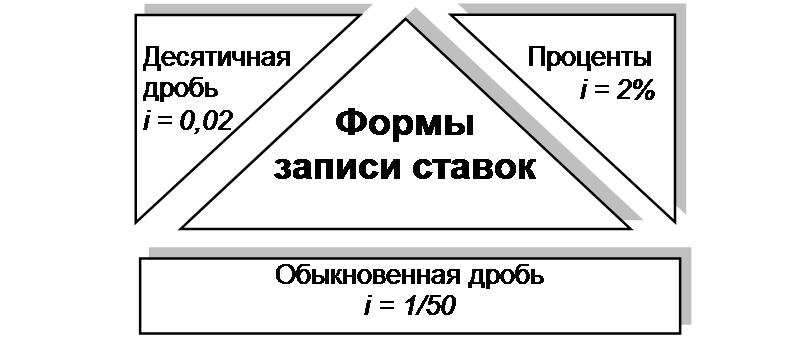
Рисунок 1.5 Формы записи ставок
![]()
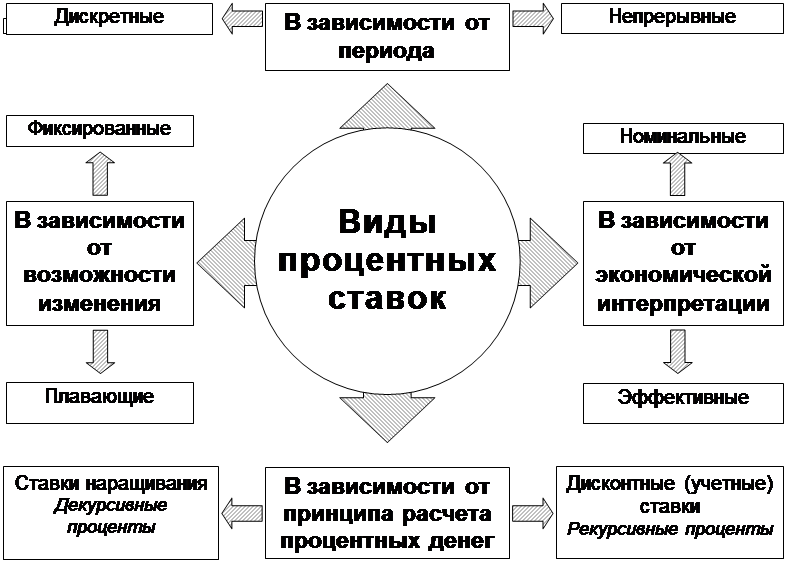
Рисунок 1.6 Виды процентных ставок
Таблица 2.1
Ставка процента и ставка дисконта
|
Ставка процента |
Ставка дисконта |
|||
|
I этап: выдача |
|

|
||
|
II этап: использование |
||||
|
III этап: возвращение |

|
|
||
2.
Таблица 2.2
Обозначения
|
Обозначения |
Смысл |
I |
проценты за весь срок |
|
P |
начальная сумма |
|
S |
наращенная сумма |
|
I |
ставка процента |
|
n |
число лет наращивания суммы |
|
m |
число периодов наращивания суммы внутри года |
|
d |
дисконтная (учетная) ставка |
Таблица 2.3
Формулы расчета простых процентов
|
Метод расчета Операция |
Простые проценты |
Пример |
Наращение |
S = P(1+ni) |
|
Дисконтирование |
P = S / (1+ni) |
|
Учет (векселей) |
P = S(1-nd) |
|
Наращение по учетной ставке |
S = P / (1-nd) |
Таблица 2.4
Расчет простых процентов для краткосрочных ссуд (меньше года)
|
Метод расчета дней в году Метод расчетадней ссуды |
Точный (365; 366) |
Приближенный(360 = 12 * 30) |
Точный(фактическое количество дней, день выдачи и день погашения первой цены) |
365/365; АСТ/АСТ |
Банковский метод (межстрановые ссудные операции), а также Франция, Бельгия, Швейцария 365/360; АСТ/360 |
Приближенный(полный месяц – 30 дней, неполный месяц – по факту) |
Коммерческие банки Германии, Швеции, Дании 360/360 |
6. «Бывший № 1»
Таблица 2.5
Формулы расчета сложных процентов
Метод расчетаОперация |
Сложные проценты |
Пример |
Наращение |
S = P(1+i)n |
|
Дисконтирование |
P = S / (1+i)n |
|
Учет (векселей) |
P = S(1-d)n |
|
Наращение по учетной ставке |
S = P / (1-d)n |
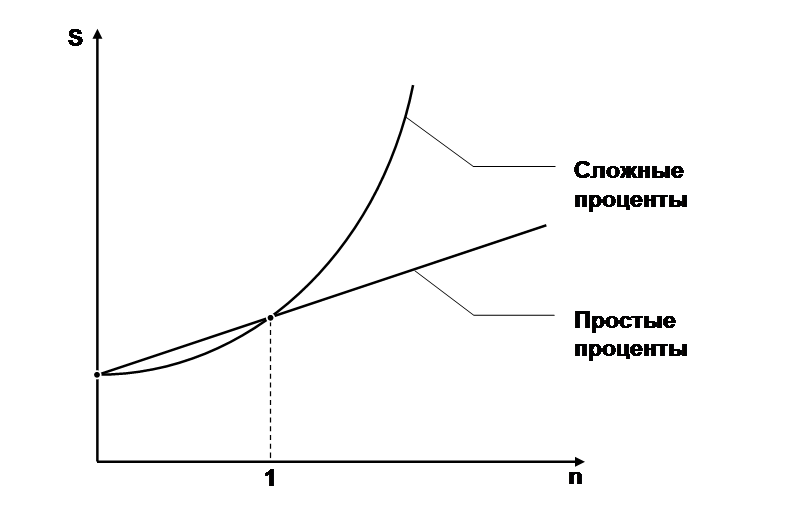
Рисунок 2.1 Сравнение силы роста простых и сложных процентов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.