Решение интегрального уравнения Фредгольма второго рода

Министерство образования Российской Федерации

Тульский государственный университет

Кафедра РЭ

Контрольно-курсовая работа

по дисциплине “Численные методы”

Выполнил: студент группы 220511  Патрин Максим Николаевич

             Проверил:                                            Полынкин А.В.

Тула 2002

Аннотация

В данной работе рассматривается решение интегрального уравнения Фредгольма второго рода. Используя метод квадратурных формул, данное уравнение раскладывается на систему из n линейных алгебраических уравнений с n неизвестными. Для нахождения интеграла используется метод прямоугольников со средним отсчетом. Интервал значений разбивается на n частей с одинаковым шагом. Полученная система решается методом Гаусса.

Задание

№ 86

Используя метод квадратурных формул, решить с тремя десятичными знаками интегральное уравнение Фредгольма второго рода

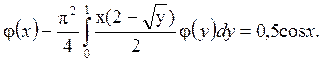
Решение

Математическая часть

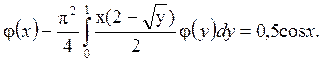                            0                        1    x,y

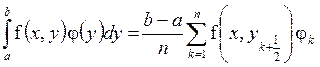                       b=1, a=0, n=5.

                                                                         i,k=        1     2      3    4      5

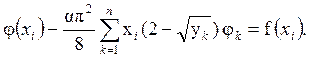
                             0 0.1  0.3   0.5  0.7  0.9 1  x,y

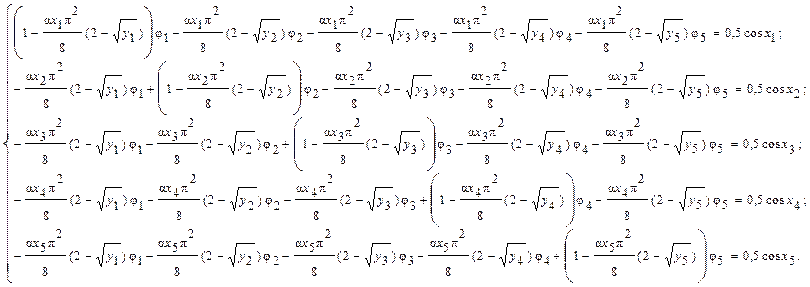
          Полученная система решается методом Гаусса. Коэффициенты при  обнуляются в последних 4 уравнениях, при  - в последних 3 уравнениях, при  - в последних 2 уравнениях и при  - в последнем уравнении, используя методы элементарных преобразований. После ряда преобразований из 5-го уравнения находим , подставляя его в 4-ое уравнение находим  . И, таким образом, подставляя найденные значения в предшествующие уравнения, находим остальные значения  .

Расчетная часть

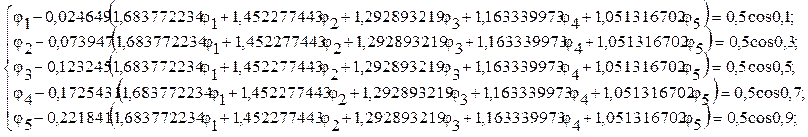
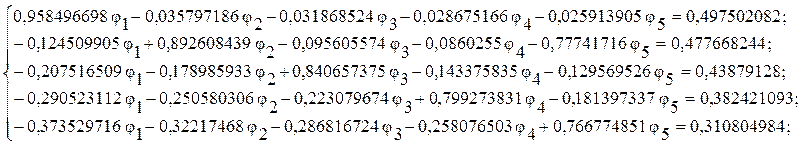
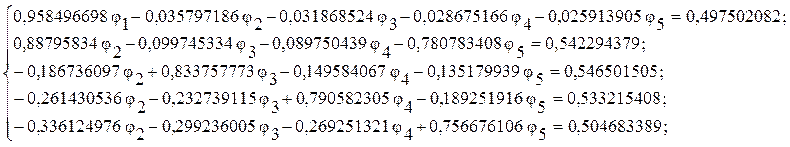
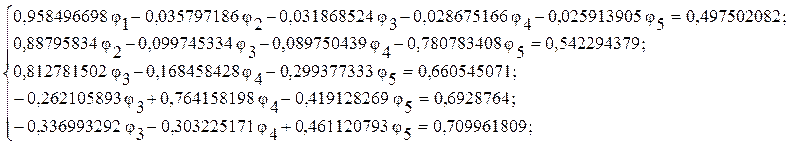
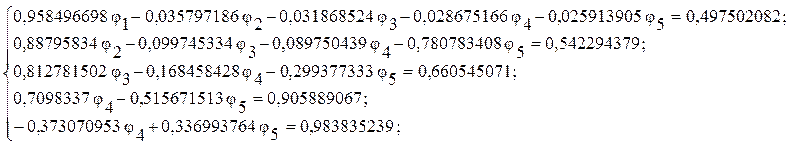
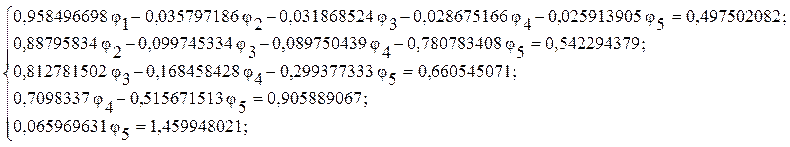
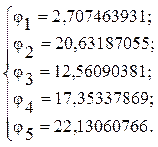
Ответ:

Заключение

          В представленной выше работе было решено интегральное уравнение Фредгольма второго рода. В ходе решения использовались:

1)  метод квадратурных формул для разложения на систему линейных алгебраических уравнений (метод, необходимый по условию задания);

2)  метод прямоугольников со средним отсчетом для нахождения интеграла;

3)  метод Гаусса для решения системы линейных алгебраических уравнений.

Ответ представлен в виде таблицы значений функции  для .

Список использованной литературы

1.  Лекции по дисциплине “Численные методы”.