Предмет и метод финансовой математики, страница 2

Таблица 2.5

Эффективная ставка наращения для различных финансовых операций

Финансовая операция	Номинальная ставка	Эффективная ставка наращения
Наращение по простым процентам	is
Учетные операции по простым процентам	ds
Учетные операции по сложным процентам	d
Наращение по сложным процентам несколько раз в год	j
Учет по сложным процентам несколько раз в год	f
Непрерывное наращение	d

Таблица 2.6

Эффективная учетная ставка для различных финансовых операций

10.

Если проценты начисляются m раз в год, то формула сложных процентов видоизменяется.

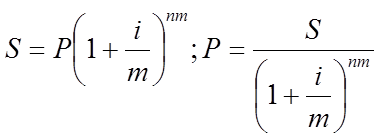
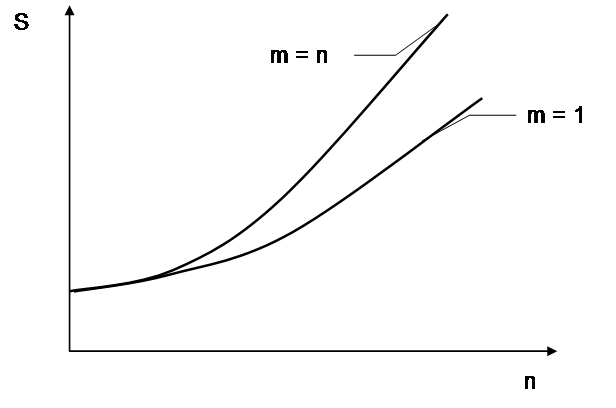
Рисунок 2.2 Сила роста и периодичность начисления процентов за период меньше года

12.

Непрерывное наращивание (формула, график)

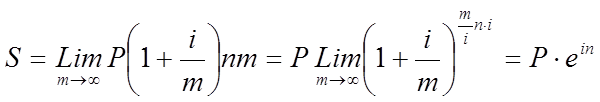
13.

Анализ формул, расчет параметров (из таблиц)

14.

Влияние инфляции на финансовые расчеты (формулы)

Таблица 2.7

Влияние инфляции на финансовые расчеты

Вид операции по начислению процентов	Расчетная формула
Простые проценты
Сложные проценты (по эффективной ставке)

15.

Сила роста различных методов начисления процентов (неравенство)

S < j < i < d < d_s < i_s

16.

Таблица 0.1

Изменяющиеся во времени ставки процентов (формулы)

Вид финансовой операции	Расчетная формула
Наращение по переменной ставке простого процента	, где it– ставка простых процентов в периоде t, nt – продолжительность периода с постоянной ставкой/
Реинвестирование по простым ставкам	S = P (1+n1i1)(1+n2i2)…(1+ntit)…, где it – размер ставок, по которым производится реинвестирование Если промежуточные сроки начисления и ставки не изменяются во времени, то формула имеет вид S = P(1+ni)m где m – количество повторений реинвестирования
Наращение по плавающей ставке сложного процента	S = P(1+i1)n1(1+i2)n2…(1+ik)nk, где i1, i2, …ik – последовательные значения ставок; n1, n2, …, nk – периоды, в течение которых «работают» соответствующие ставки.

17.

 

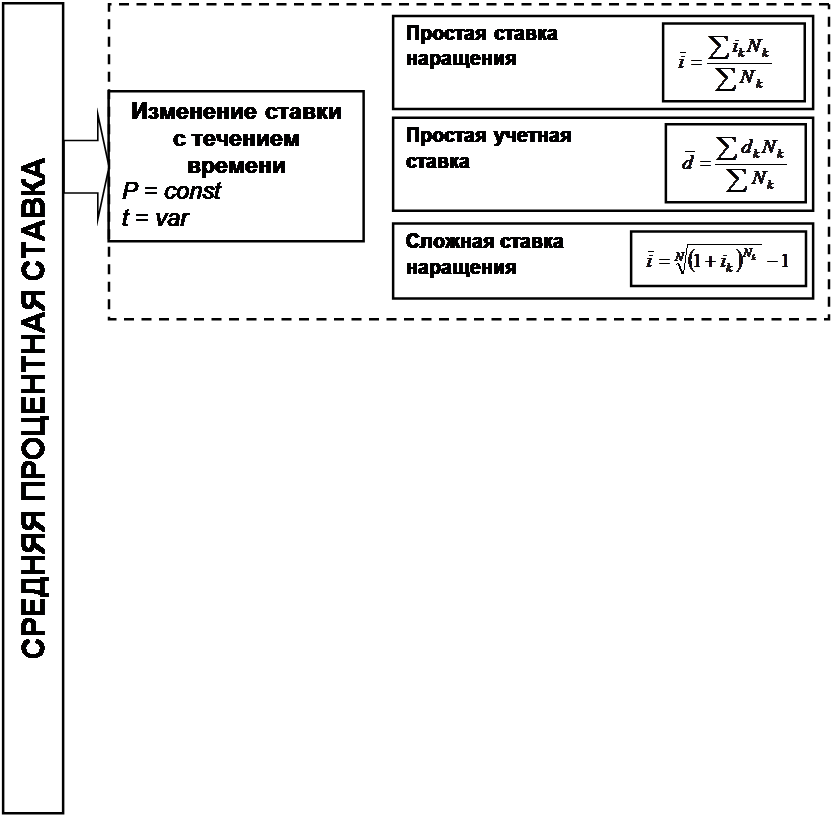
Рисунок 0.1

18.

Эквивалентность процентных ставок

 

Рисунок 0.2

19. Эквивалентность денежных сумм (схема)

Тема 3

Поток платежей (cash flow stream) – последовательность платежей и моментов времени, в который они были осуществлены.

Величина потока в момент времени T – приведенная к моменту Т величина всех платежей потока R(T).

Величина потока в начальный момент времени называется современной величиной потока.

Величина потока в конечный момент времени – приведенная величина потока.

Таблица 0.1

Обозначения