Вычисление максимума (минимума) скалярной целевой функции. Структура оптимизатора целевой функции (Глава 11 Методики применения пакета Mathcad для решения научных и типовых общетехнических задач)

11. Вычисление максимума (минимума) скалярной целевой функции. Структура оптимизатора целевой функции

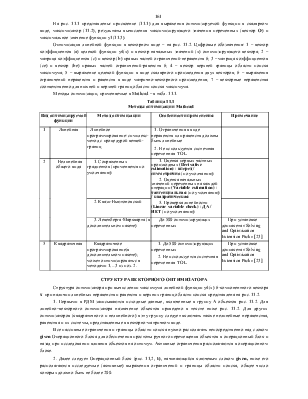
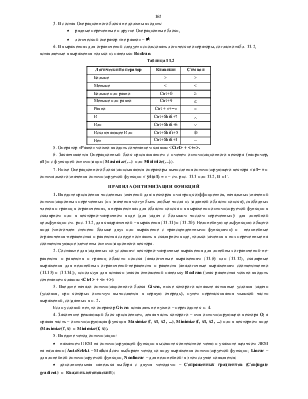
Формирование структуры оптимизатора. Решение задач линейного и квадратичного программирования.

Ключевые термины раздела 11.

квадратичное программирование – оптимизация квадратичной цельфункции.

линейное программирование – оптимизация линейной цельфункции.

область поиска оптитмума –  неравенства, ограничивающие снизу и сверху значения переменных оптимизации.

ОГРАНИЧЕНИЯ В ЗАДАЧАХ ОПТИМИЗАЦИИ – линейные и нелинейные неравенства и равенства, связывающие оптимизационные переменные.

ОПЕРАЦИОННЫЙ БЛОК – позиционная совокупность объектов Mathcad, начинающаяся системным словом given и заканчивающаяся одной из оптимизационных функций Maximize(…)  или Minimize(…), между которыми расположены различные ограничения и выражения для диапазонов оптимизируемых переменных.

оптимизатор – решатель, обеспечивающий вычисление оптимума (максимума или минимума) цельфункции, включающий: целевую функцию, начальные значения оптимизирующих переменных, операционный блок, выражения для значений оптимизирующих переменных и оптимального значения цельфункции, выдаваемых Mathcad в результате решения оптимизационной задачи. Может иметь скалярную или векторную формы.

скалярная форма оптимизатора – переменные оптимизации являются независимыми переменными, ограничения-неравенства и равенства записываются в виде систем неравенств и уравнений соответственно.

векторная форма оптимизатора – переменные оптимизации являются компонентами оптимизационного вектора, ограничения-неравенства и равенства записываются в векторно-матричной форме. Эта форма многократно компактнее скалярной и значительно сокращает трудоемкость решения оптимизационной задачи.

целеавя функция (цельфункция) – скалярная или векторнаяфункция, численно характеризующая цель определенной стратегии, операции или плана действий.

11.1. Вычисление оптимума целевой функции

Вычисления производятся посредством функций Maximize(…)  и Minimize(…), записываемых в составе оптимизаторов (максимизатора или минимизатора соответственно) в скалярном виде (Maximize(f, х1, х2, ...)  и Minimize(f, х1, х2, ...) или в векторном (Maximize(f, х)  и Minimize(f, х)),  в которых f – имя оптимизируемой скалярной функции из присвоения, записанного выше решающего блока (в присвоении функция записывается вместе со списком ее аргументов-переменных в круглых скобках: f(х1, х2, ...) – для скалярной записи; f(х) – для векторной), х1, х2, ... – скалярные, х – векторная переменные, по которым производится оптимизация.

В прикладных задачах оптимизируемая функция называется целевой. Одна из наиболее общих содержательных постановок задачи оптимизации скалярной целевой функции f(х) – векторная запись:

при следующих линейных и нелинейных ограничениях и условиях:

А × х £ b  - линейные неравенства,

Аeq × х = beq  - линейные равенства,(11.0)

C(x) £ 0  - нелинейные неравенства,

Ceq(x) = 0  - нелинейные равенства,

Lb £ x £ Ub - область поиска оптимума,