Вычисление максимума (минимума) скалярной целевой функции. Структура оптимизатора целевой функции (Глава 11 Методики применения пакета Mathcad для решения научных и типовых общетехнических задач), страница 6

Пример решения задачи квадратичного программирования для 7-компонентного вектора в векторной записи с применением нелинейных ограничений (неравенства и равенства) представлен на рис. 11.3. Задача решена методом Сопряженных градиентов (Conjugate gradient), автоматически выбранным Mathcad  (квази-ньютоновский метод дает тот же результат).

На рисунке: исходные данные (11.10) представлены в векторном и матричном видах; целевая функция у6(х) (11.11), линейные ограничения и границы области поиска записаны в векторно-матричном виде (11.12); нелинейные ограничение-неравенство (11.13) и равенство (11.14) записаны в скалярном виде с заменой независимых переменных хN на соответствующие компоненты вектора х_N. Показано решение одной из задач оптимизации – поиск максимума целевой функции у6(х) при наличии линейных ограничений-неравенств, верхней границы области поиска оптимума и нелинейных ограничений: неравенства (11.13) и равенства (11.14). Решение представлено оптимизирующим вектором о5 и максимальным  значением цельфункции у6(о5).

 

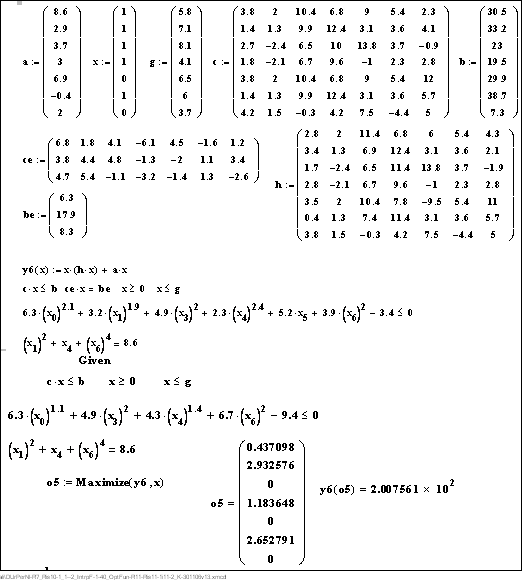                                                                                                                                                                        (11.10)

(11.11)

(11.12)

(11.13)

(11.14)

 

                                                                                                                                                                         (11.15)

Рис. 11.3.  Определение максимума квадратичной функции у6(х) (11.11) в векторно-матричном виде с исходными данными (11.10) в частной задаче при наличии линейных ограничений-неравенств и нижней и верхней границ области поиска (вторая строка оперблока (11.15)) и нелинейных неравенства и равенства – третья и четвертая строки оперблока)

Правила оптимизации квадратичной функции – см. в разд. 11.1                                                                         (с учетом следующих примечаний)

Примечания

1. Целевую функцию, линейные ограничения и ограничения на область поиска оптимизационного вектора целесообразно при оптимизации представлять в векторно-матричном виде.

2. Пример приведения целевой функции от скалярного к векторно-матричному виду при исходном выражении, отличном от 11.9:

z11(х0,…,х5) = [m00х0²+m11х1² +m22х2²+m33х3² +m44х4² +m55х5² +m66х6² + m01х0х1 + m02х0х2+ m03х0х3+ m04х0х4+m05х0x5+ m12х1х2 + +m13х1х3 + + m14х1х4+m15х1x5 + m23х2х3 + m24х2х4+m25х2x5+ m34х3х4+m35х3x5+m45х4x5] +а0х0+ а1х1+ а2х2 + а3х3 + а4х4 + a5x5,                                                           (11.16)

где xi (i=0…5) – переменные, mij, ai – наборы чисел.  

Представим z11(х) в виде (умножив каждый член квадратной скобки на 2 и всю скобку – на 0,5):

z11(х0,…,х5) = 0.5[2m00х0²+2m11х1² +2m22х2²+2m33х3² +2m44х4² +2m55х5² +2m66х6² + 2m01х0х1 + 2m02х0х2+ 2m03х0х3+ 2m04х0х4+2m05х0x5+ 2m12х1х2 + +2m13х1х3 + + 2m14х1х4+2m15х1x5 + 2m23х2х3 + 2m24х2х4+2m25х2x5+ 2m34х3х4+2m35х3x5+2m45х4x5] +а0х0+ а1х1+ а2х2 + а3х3 + а4х4 + a5x5.             (11.17)