Вычисление максимума (минимума) скалярной целевой функции. Структура оптимизатора целевой функции (Глава 11 Методики применения пакета Mathcad для решения научных и типовых общетехнических задач), страница 5

3. Введите начало оптимизационного блока Given, ниже котороговставьте активные условия задачи (условия, при которых оптимум вычисляется в первую очередь), путем перетаскивания мышкой части выражений, созданных в п. 2.

Если условий нет, то оператор Given  вставлять не нужно – переходите к п. 4.

4. Закончите решающий блок присвоением, левая часть которого – имя оптимизирующего вектора О, а правая часть – оптимизирующая функция Maximize(f, х1, х2, ...), Minimize(f, х1, х2, ...) или в векторном виде (Maximize(f, х)  и Minimize(f, х)).

5. Введите метод оптимизации:

·  нажатием ПКМ на оптимизирующей функции вызовите контекстное меню и укажите щелчком ЛКМ на названии (AutoSelekt – Mathcad сам выбирает метод по виду выражения оптимизируемой функции; Linear – для линейной оптимизируемой функции, Nonlinear – для нелинейной: в этом случае появляется;

·  дополнительная панелька выбора с двумя методами – Сопряженных градиентов (Conjugate gradient)  и  Квази-ньютоновский);

·  нажатием на второй панельке команды Advanced Options  можно изменить параметры Особенности применения, установленные по умолчанию  – см. табл. 11.1; эта возможность используется в случае отсутствия решения с параметрами по умолчанию.

6.В ответ на ввод имени вектора О оптимизирующих переменных и нажатие клавиши <= +> Mathcad выдает вектор значений оптимизирующих переменных в том порядке, в каком они перечислены в оптимизирующей функции.

7. Для вычисления оптимального значения функции f необходимо вставить ее вычисление, заменив переменные в ее имени соответствующими компонентами оптимизирующего вектора О (для нелинейной цельфункции – см. 11.3)или самим вектором О (для линейной или квадратичной цельфункции – см. 11.7 или 11.11).

8. Если стоит задача исследовать влияние сочетаний различных ограничений и границ области поиска на оптимум, то следует в Word-документе создать шаблон Таблицы результатов оптимизации, аналогичный табл. 8.1 из задания 8 разд. 14, в которой каждому сочетанию будет соответствовать своя строка и номер задачи . При наличии нелинейных ограничений шаблон нужно дополнить столбцами с этими ограничениями и дополнительными строками для сочетаний линейных ограничений с нелинейными.

9. Для решения каждой задачи из Таблицы результатов следует делать активными те ограничения и границы, в столбцах которых стоит знак « + », т.е. объекты Mathcad, соответствующие ограничениям в рассматриваемом сочетании, нужно переместить в Операционный блок. Решение, выданное  Mathcad (оптимизирующий вектор и оптимальное значение цельфункции) помещают в ячейки результата задачи. Если решение не найдено, в эти ячейки помещается запись «нет решения (нр)».

11.2. Задача линейного программирования                          (линейная цельфункция)

В этой задаче Целевая функция f(x) и ограничения – должны быть линейными, т.е. из общей постановки (11.0) должны быть удалены нелинейные ограничения с C(x)  и Ceq(x).

Правила оптимизации указаны выше.

Пример решения задачи линейного программирования в векторной записи представлен на рис. 11.2.

11.3. Задача квадратичного  программирования                           (квадратичная цельфункция)

В этой задаче Целевая функция f(x) – квадратичная, вида (в векторной форме)

у6(х) =x^T ×h× х + а× х или в символике Mathcad:  x ×(h× х) + а× х                                                                   (11.8)

где x и а – векторы одинаковой размерности N, а hm – NxN - матрица. В скалярном виде:

у6(х₁, …, х_N) = 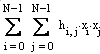                                + а₀× х₀ + …+ а_N× х_N.                                                                               (11.9)