Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Системного Анализа и Управления
Работа №1
Курс: «Вычислительная математика»
Тема: «Интерполирование функций»»
Вариант 5
Выполнил: ст. гр. 2082/2
Дегтярёв И. В.
Проверил: Куприянов В. Е.
Санкт-Петербург
2006 г.
1. Постановка задачи.
Сравнить графики интерполяционных полиномов в форме Ньютона Pn(x) (n = 2, 6, 14) с заданной функцией f(x) при двух вариантах выбора узлов:
а) равномерно с шагом h = 2/n
б) по Чебышеву
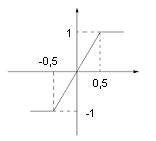
2. Метод решения.
Выбор узлов по Чебышеву:
x = cos((2i + 1)π/2n))
Кусочно-линейный сплайн:
f(x) = a1 + a2x + α1|x – x1| + α2|x – x2|
Разделенные разности:
f(x0,…, xn) = (f(x1,…,xn) – f(x0,…,xn-1))/(xn – x0)
Интерполяционный полином в форме Ньютона:
Nn(x) = f(x0) + (x - x0)f(x0, x1) +…+ (x - xn-1)f(x0, x1, xn)
3. Структура программы.
1) i_pol = main(n, type)
Входные значения: n – степень полинома
type – тип выбора узлов
Выходные значения: i_pol – массив значений и.п.
function i_pol = main(n, type)
x_m = razb(n, type); %а)
f = zn_func(x_m); %б)
rr_m = rr(f, x_m, n); %в)
i_pol = pol(rr_m, x_m, n); %г)
2) а) x = RazbFn(n, type)
Входные значения: n – степень полинома
type – тип выбора узлов
Выходные значения: x – массив разбиения
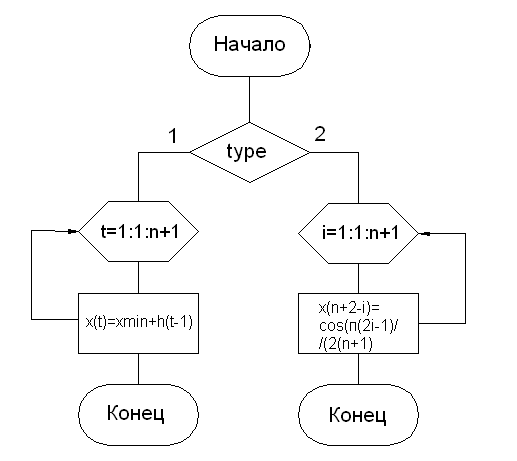
б) f = zn_func(x)
Входные значения: x - разбиение
Выходные значения: f – массив значений функции
в) rr = RR(f, x, n)
Входные значения: f – массив значений функции
x - разбиение
n – степень полинома
Выходные значения: rr – массив разделенных разностей
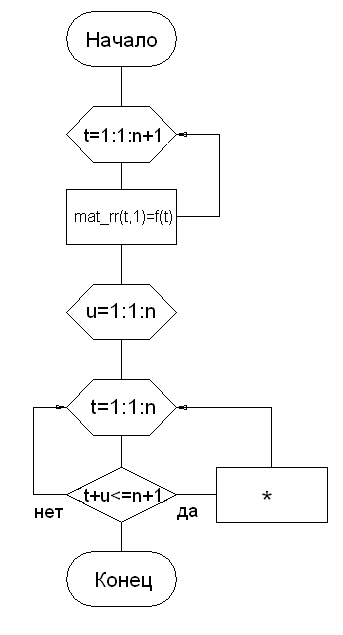
(*) mat_rr(t, u + 1) = (mat_rr(t + 1, u) - mat_rr(t, u))/(x(t + u) - x(t))
г) i_pol = pol(rr_m, x_m, n)
Входные значения: rr_m – массив разделенных разностей
x - разбиение
n – степень полинома
Выходные значения: i_pol – массив значений и.п.
3) megamain()
Вызывает несколько раз функцию main для построения графиков с различными значениями n и type.
4. Текст программных модулей.
function megamain()
n = [2, 6, 16];
x = [-1: 0.01: 1];
for t = 1: 1: 3
subplot(2, 2, t);
zf = zn_func(x);
pr = main(n(t), 1);
pch = main(n(t), 2);
plot(x, zf, x, pr, x, pch, x, zf - pr, x , zf - pch), grid on;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.