






Курс лекций по дисциплине «ТВиМС»
|
4. Элементы теории случайных процессов |
– 2 часа |
|
Л.11. Случайный процесс. Случайный поток событий. Простейший поток событий. Суперпозиция нескольких простейших потоков. Прореживание простейшего потока. |
– 2 часа |
План:
· Приветствие;
· Краткие сведения из материала, изучаемого на прошлой лекции;
· Понятие о случайном процессе;
· Случайный поток событий. Простейший поток событий
· Распределение количества событий простейшего потока, на некотором временном интервале
· Теоремы о случайном и регулярном прореживании простейшего потока событий;
· Теоремы о суперпозиции простейших потоков событий;
· Послесловие. Задание на дом.
Иногда на практике приходится иметь дело со случайными явлениями, протекание которых во времени непредсказуемо и в каждый момент времени описывается случайной величиной.
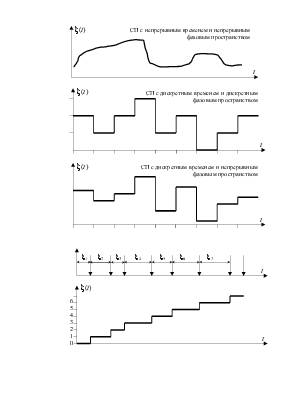
Случайным процессом называется функция x(t) неслучайного аргумента t (как правило, времени), которая при каждом фиксированном значении аргумента является случайной величиной. Пример: температура в течение суток, регистрируемая самописцем; значение уровня помехи во времени; количество посетителей в магазине в течение рабочего дня; население Земли.
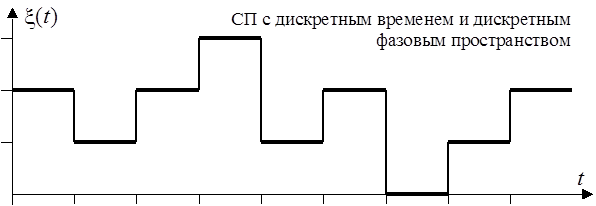
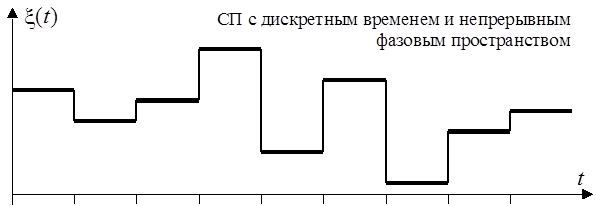
Значения, принимаемые процессом x(t) в определенные моменты времени называются состояниями, а множество всех состояний – фазовым пространством случайного процесса. Фазовое пространство может быть дискретным или непрерывным.
Если СП может изменять своё состояние лишь в определённые моменты времени, то такой процесс называется СП с дискретным временем; а если в любые (случайные моменты), то – с непрерывным временем.
Примеры:
x(t) – число на кости при ежесекундном подбрасывании;
x(t) – количество подключений к Internet серверу во времени;
x(t) – температура, регистрируемая каждый час; регистрируемая постоянно;
x(t) – состояние микропроцессора (синхронного дискретного устройства).

Случайный поток событий. Простейший поток событий
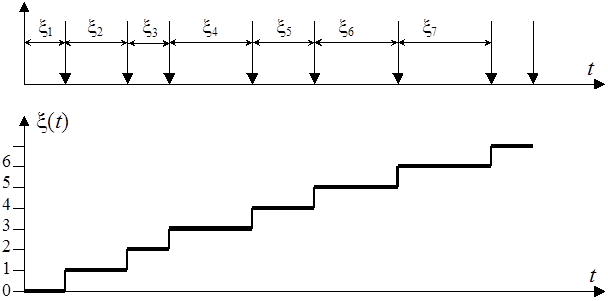
Потоком событий называется последовательность событий (как правило, однотипных), происходящих одно за другим в какие-то моменты времени.
Поток событий описывается набором величин x1 – времени до первого события потока, x2 – временем между первым и вторым событием потока и т.д. до бесконечности.
ПРИМЕРЫ:
1. поток отказов ЭВМ,
2. поток покупателей в магазин,
3. поток заявок на АТС,
4. поток студентов в гардероб,
5. поток посещений Internet сервера;
6. поток электричек в метро,
7. поток посетителей ЖД кассы (в часы её работы).
СП по существу является случайным процессом, где x(t) – число событий потока, поступивших к моменту времени t.
Если xi – есть СВ, то поток событий является случайным, в противном случае – детерминированным или регулярным.
В вероятностном смысле случайный поток описывается множеством распределений СВ времени до первого события потока и между событиями.
Если закон распределения СВ xi одинаковый, то такой случайный поток называется рекуррентным потоком без запаздывания.
Когда мы говорили о случайных явлениях, то упоминали лишь СС,СВ и СП. Случайный поток, по сути, является СП x(t) со счетным множеством состояний, где x(t) – число событий потока, произошедших к моменту времени t.
Подробнее о случайных потоках: (Вентцель - Теория вероятностей 5-е изд.1998; Малинковский – ТМО м.п.)
Сейчас же мы рассмотрим потоки событий, обладающие некоторыми свойствами.
1. Случайный поток событий (СПС) называется стационарным, если вероятность наступления некоторого числа событий на участке времени длиной t зависит только от длины участка и не зависит от того, где именно на оси времени расположен этот участок.
2. СПС называется потоком без последействия, если для любых не перекрывающихся участков времени число событий, попадающих на один из них не зависит от числа событий, попадающих на другие.
3. СПС называется ординарным, если вероятность попадания на элементарный участок dt двух и более событий пренебрежимо мала по сравнению с вероятностью попадания только одного события.
СПС, обладающий всеми тремя свойствами, называется простейшим. Простейший поток событий характеризуется интенсивностью, т.е. средним числом событий, наступающих в единицу времени.
ПРИМЕР: на вышеприведенных примерах рассмотреть указанные свойства.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.