Простейшие потоки играют в ТВ и ТМО особую роль. Во-первых, указанными свойствами обладает большая часть реальных потоков событий в жизни. Во-вторых, сумма большого числа ординарных, стационарных потоков с любым последействием образует поток, сколь угодно близкий к простейшему.
НАПРИМЕР: поток отказов ЭВМ складывается из потока отказов CPU, MEMORY, SystemBoard, Контроллеров, накопителей и прочее. Тогда можно говорить о простейшем потоке отказов ЭВМ.
В третьих, исследование простейших потоков очень не сложно, и уже практически полностью создана теоретическая база исследования простейших потоков.
Распределение количества событий простейшего потока, на некотором временном интервале
Интенсивностью l простейшего потока называют среднее число событий потока, происходящих в единицу времени. В силу стационарности ППС l=const.
Выделим на оси времени отрезок длины T и рассмотрим ДСВ h – число событий ППC, попавших в этот отрезок. Очевидно, что x=0,1,2… Вычислим вероятность того, что на отрезок T придется ровно k событий.
Для этого разобьём отрезок T на n®¥ элементарных участков длины dt®0.
В силу стационарности простейшего потока l=const.

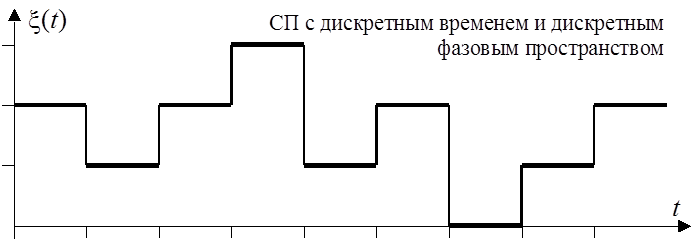
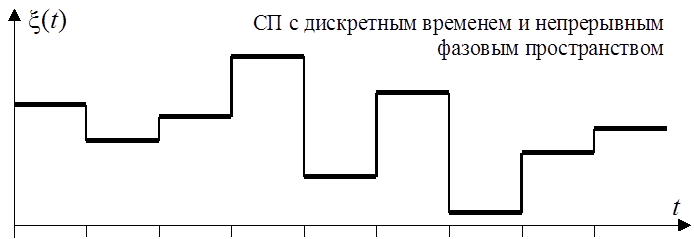
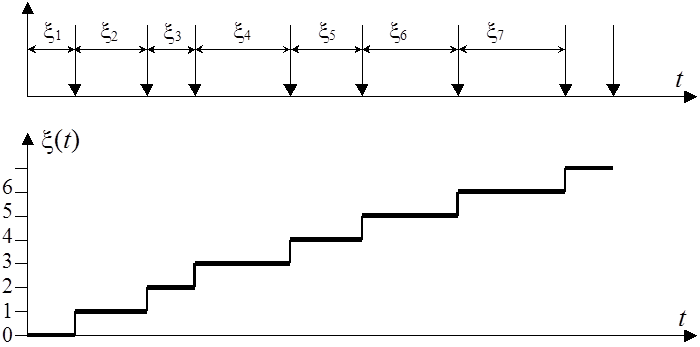
Распределение количества событий простейшего
потока
событий, на некотором временном интервале
Интенсивность простейшего
потока событий (ППС) l – среднее
число событий потока, происходящих в единицу времени ![]()
Пусть h – случайная величина числа событий ППС на некотором временном интервале T; h=0,1,2… Вычислим вероятность того, что на этот отрезок попадёт k событий. Разобьём отрезок T на n®¥ элементарных участков длины dt®0.
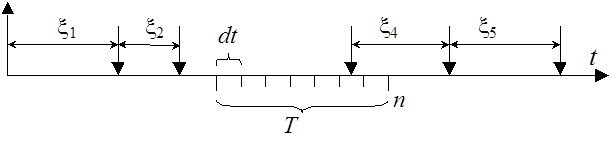
В силу ординарности ППС вероятностью попадания на один элементарный участок dt сразу нескольких событий потока пренебрежём.
В силу стационарности и отсутствия последействия ППС, вероятность попадания одного события потока на элементарный участок dt не изменяется и не зависит от того, как события потока наступали в прошлом.
Следовательно, наступление событий в каждом из n элементарных участков можно рассматривать как схему n®¥ испытаний Бернулли, где «успех» – попадание события ППС в некоторый элементарный участок dt, вероятность «успеха» p®0.
Тогда по предельной
теореме Пуассона количество событий ППС с интенсивностью l на некотором временном интервале T,
имеет распределение Пуассона с параметром lT:
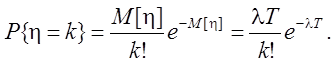
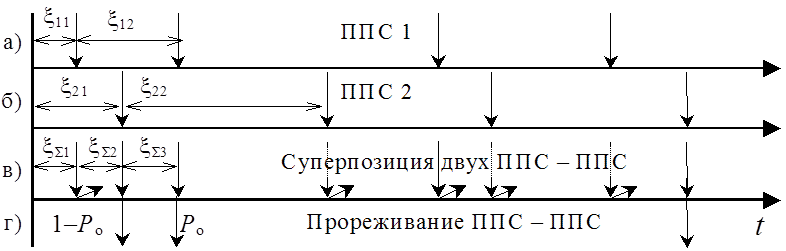
Рисунок – Суперпозиция и прореживание простейшего потока событий
Суперпозиция независимых простейших потоков
Пусть на некоторый объект воздействует n независимых простейших потоков. Например, поток отказов ЭВМ складывается из потока отказов CPU, MEMORY, SystemBoard, Контроллеров, накопителей и прочего оборудования, а также программного обеспечения.
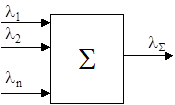
Требуется определить характеристики суммарного потока событий.
Рассмотрим эту задачу для случая двух исходных простейших потоков событий: первый поток (рисунок _а) имеет интенсивность l1, а второй (рисунок _б) – интенсивность l2. Пусть xij – время между (j–1) и j-тым событиями i-того потока событий (см. рисунок _а и _б).
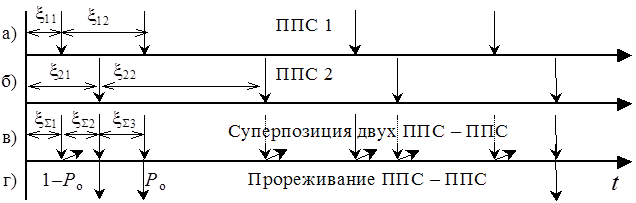
Рисунок _
Время xS1 до первого события потока, образованного суперпозицией двух потоков событий, очевидно из рисунка _, равно минимальному из значений x11 и x21, т.е. xS1=min{x11 , x21}. Поскольку простейший поток событий является потоком без последействия (не важно, сколько и каким образом наступали события простейшего потока к моменту времени To, время до наступления очередного события имеет показательный закон распределения с параметром l), то время до очередного события результирующего потока определяется соотношением:
xS=min{x1 , x2},
где xS – случайная величина времени между событиями результирующего потока событий; x1 – случайная величина времени между событиями первого простейшего потока событий; x2 – случайная величина времени между событиями второго простейшего потока событий. Здесь следует вспомнить, что ППС является рекуррентным потоком без запаздывания.
Известно, что x1~E(l1), а x2~E(l2), следовательно Fx1(x)=P(x1<x)=1–exp(–l1×x), а Fx2(x)=P(x2<x)=1–exp(–l2×x). Закон распределения случайной величины xS требует определения, т.е. FxS(x)=P(xS<x)=?
Рассмотрим вероятность события {xS³x}, противоположного к событию {xS<x}. P(xS³x)=P(min{x1 , x2}³x)=P({x1³x}Ç{x2³x}), поскольку чтобы меньшая из величин была больше или равна x, необходимо, чтобы каждая из величин была больше или равна x.
Поскольку два исходных потока являются независимыми (по условию), то независимыми являются события {x1³x} и {x2³x}. Следовательно, применяя теорему умножения вероятностей независимых событий:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.