Основы математической статистики: Методические указания к расчетному заданию по курсу "Теория вероятностей и математическая статистика", страница 5

          Случайная  величина Т подчинена закону распределения Стьюдента
с n-2 степенями свободы. При достаточно большом числе степеней свободы  закон распределения Стьюдента стремится к нормальному закону, при этом  . Следовательно, в этом случае уровень значимости гипотезы об отсутствии корреляционной связи между случайными величинами  X  и  Y  может быть определен по выражению

                                                 

где .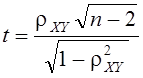

          Если q < 0.05, то гипотеза об отсутствии корреляционной связи между величинами X и Y отвергается. В этом случае следует определить доверительный интервал для .

3.4.3. Определение доверительного интервала

для оценки коэффициента корреляции

          Доверительная вероятность попадания коэффициента корреляции в интервал  определяется выражением

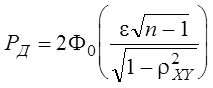          .                                  (3.23)

          Относительная ширина интервала составляет

                                                  .

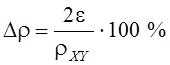3.4.4. Определение параметров линейной регрессии

Поставим задачу определения статистических оценок параметров линейной регрессии случайной величины  Y  на  Х:

                                                  M [Y/x] = .                                       (3.24)

Статистическая оценка регрессии запишется в виде:

                                                  ,                                             (3.25)

где  b₀  и  b₁ – статистические оценки коэффициентов линейной регрессии;

            – статистическая  оценка  условного  математического  ожидания

                        СВ Y.

          Коэффициенты b₀ и b₁ могут быть определены с помощью метода наименьших квадратов: значения этих коэффициентов должны минимизировать сумму квадратов отклонений эмпирических значений y_j от прямой, описываемой уравнением (3.25). На рис. 3.3 эмпирические значения y_j обозначены дискретными значками, линия регрессии – сплошной линией.

 

Рис. 3.3.  К пояснению метода наименьших квадратов

Согласно методу наименьших квадратов коэффициенты b₀ и b₁ определяются из выражений:

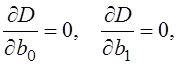                                                                                        (3.26)

где .

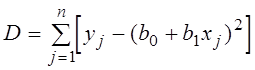Условиям (3.26) отвечают следующие выражения для коэффициентов:

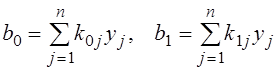                                      ,                                (3.27)

где          ,     .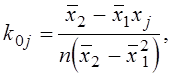

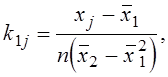
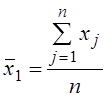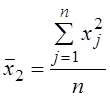Статистическая значимость построенной линии регрессии может быть оценена с помощью двустороннего критерия Фишера. В рассматриваемой задаче критерий Фишера при условии, что  , формируется как

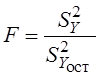                                                ,                                                    (3.28)

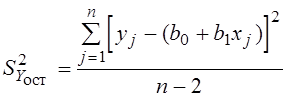 – остаточная дисперсия (показатель ошибки предсказания уравнением регрессии результатов опыта);

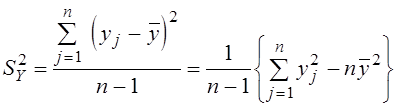 – дисперсия выборки  .

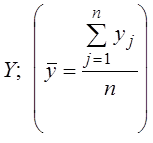Уровень значимости гипотезы о правомочности построенной линии регрессии зависит от величины критерия F è чисел степеней свободы сумм числителя n₁ = (n–1) и знаменателя n₂ = (n–2) в выражении (3.28). В рассматриваемом расчетном задании n = 20. Значения уровня значимости â этом случае, заимствованные из [3], приведены в табл. 3.3  и на рис. 3.4.

Т а б л и ц а  3.3

q = j(F, n₁ =19,  n₂ = 18)

Так, например, в случае выборки, для которой построена линейная регрессия, приведенная на рис. 3.3, F = 1.3  и  q = 0.58. Следовательно, гипотеза î линейности регрессии Y  на  X  не противоречит располагаемому статистическому материалу с уровнем значимости  q = 0.58.

 

Ðèñ. 3.4   Уровни значимости при

Литература

1.  Справочник по специальным функциям / Под ред. М. Абрамовица
и  И. Стиган. – М.: Наука. – 1979. – 825 с.

2.  Митропольский А.К. Техника статистических вычислений. – М.: Наука. – 1971. – 576 с.

3.  Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука. – 1965. – 464 с.

4.  Смирнов Н.В., Дунин–Барковский И.В. Курс теории вероятностей и математической статистики: – М.: Наука. – 1965. – 511 с.