Основы математической статистики: Методические указания к расчетному заданию по курсу "Теория вероятностей и математическая статистика", страница 3

причем в качестве числителя () берут большую из оценок  и  ( – меньшая из этих оценок).

          F – распределение зависит лишь от чисел степеней свободы:

          n₁ = n₁ – 1,  n₂ = n₂ – 1.

          Уровень значимости гипотезы о равенстве дисперсий двух выборок определяется как

                                        ,            (3.9)

где F (n₁, n₂, F_набл) – функция распределения случайной величины с n₁ è n₂ степенями свободы, подчиненной закону Р. Фишера

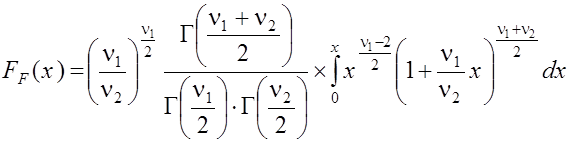                    ,    (3.10)

где 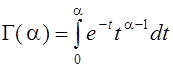  – гамма-функция                                                       (3.11)

          Зависимость  уровня значимости  q от критерия F при n_x = n_y = 20.
(n₁ = n₂ = 19) приведена на рис. 3.1.

          Следует отметить, что уровни значимости правдоподобия одной и той же гипотезы о принадлежности двух выборок Х^* и Y^* единой генеральной совокупности, определенные при использовании трех разных критериев, различны. Однако при достаточных объемах выборок это различие не является существенным и, как правило, использование различных критериев приводит к одному и тому же выводу о правдоподобии или неправдоподобии выдвинутой гипотезы.

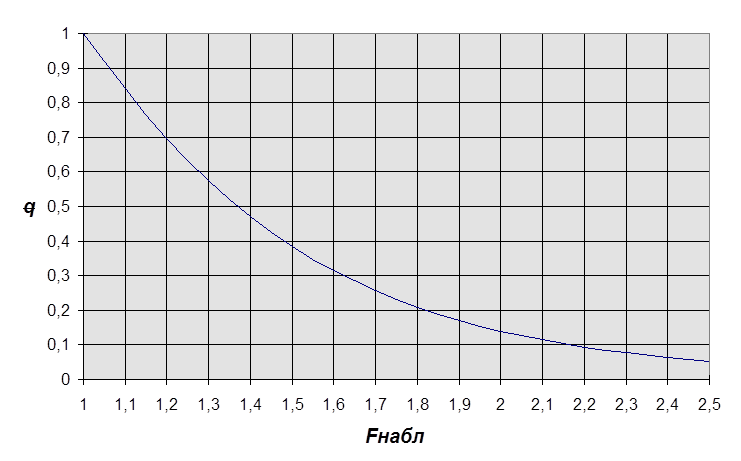
Рис. 3.1.  Зависимость  q  от  F_набл  при n_x = n_y = 20

3.3.  Проверка гипотезы о виде закона распределения

генеральной совокупности  Z

3.3.1.  Критерий Пирсона (c²) [4]

          При выполнении задания выдвигается гипотеза о нормальном законе распределения генеральной совокупности Z, представителем которой является рассматриваемая объединенная выборка Z^*. Правдоподобие этой гипотезы проверяется с помощью двух критериев: Пирсона (c²) и Мизеса (nw²). При использовании критерия согласия Пирсона необходимо весь диапазон значений   объединенной  выборки  Z  разбить  на  интервалы  D_i = z_i+1 - z_i, i=1, 2,…, k ()  и  определить число m_i членов выборки, попадающих
в i-й интервал.

          Наблюденное значение критерия определится как

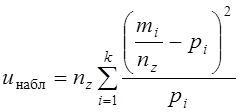          ,                                       (3.12)

где  p_i – вероятность попадания в i-й интервал при принятом гипотетическом (в настоящем задании нормальном) законе распределения генеральной совокупности.

          При гипотетическом нормальном законе вероятность p_i определяется как

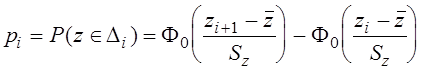          .                   (3.13)

          Результаты предварительных вычислений при применении критерия c² целесообразно представлять в табличной форме (табл. 3.1).

Т а б л и ц а  3.1

К использованию критерия Пирсона (c²)

		z2…z3	…..	zi…zi+1	…..
mi	m1	m2		mi		mk
						0.5
	-0.5
pi	p1	p2		pi		pk

          Критерий Пирсона является односторонним критерием, при этом случайная величина 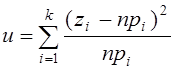 (z – случайное число попаданий значений генеральной совокупности в i-й интервал) распределена по закону c²
с  r = k - 1 - h степенями свободы (h – число параметров гипотетического закона, определенных на основе объединенной выборки). При гипотезе о нормальности  закона   распределения  генеральной   совокупности  h = 2  и  r = k - 3. Уровень значимости выдвинутой гипотезы при использовании критерия Пирсона определится как

                                                  .                                    (3.14)

Закон распределения Пирсона может быть выражен через интеграл Лапласа:

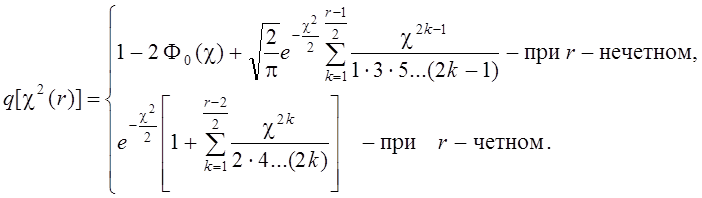   (3.15)

          Из выражений (3.15), в частности, следует:

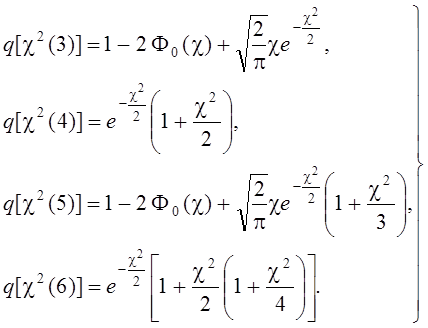                   (3.16)

Функция Лапласа Ф₀(х) может быть вычислена по следующему приближенному выражению:

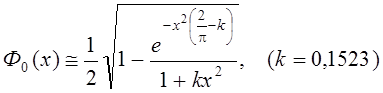.                         (3.17)

(Погрешность при использовании выражения (3.17)  при 0 < x < 5,327 не превышает 1 %.)

3.3.2.  Критерий Мизеса (nw²) [4]