Основы математической статистики: Методические указания к расчетному заданию по курсу "Теория вероятностей и математическая статистика"

Министерство общего и профессионального образования

Российской Федерации

Новосибирский государственный технический университет

========================================================

ОСНОВЫ  МАТЕМАТИЧЕСКОЙ  СТАТИСТИКИ

Методические указания к расчетному заданию

по курсу "Теория вероятностей

и математическая статистика"

для студентов II курса факультета энергетики

по направлению "Электроэнергетика"

Новосибирск

1999

Составили:  д-р техн. наук, проф. К.П. Кадомская,

                     канд.техн. наук, доц. Н.Ф. Петрова

Рецензент:  канд.техн. наук, доц. Н.В. Щеглов

Работа подготовлена кафедрой техники и электрофизики

высоких напряжений

Ó  Новосибирский государственный

        технический университет, 1999 г.

1. ЦЕЛЬ РАСЧЕТНОГО ЗАДАНИЯ

          Ознакомление с основными задачами, решаемыми методами математической статистики:

          – определением оценок числовых характеристик случайных величин и их систем;

          – оценкой точности и надежности этих характеристик;

          – проверкой правдоподобия различных гипотез: об объединяемости двух выборок; о подчинении данного статистического материала некоторому закону распределения; о наличии или отсутствии корреляционной связи между случайными величинами;

          – определением коэффициентов линейной регрессии случайных величин Х и Y и оценкой ее статистической значимости.

          Статистической обработке подвергаются две выборки случайных величин  Х^* и  Y^* объемом  n_x = n_y = n.

2. СОСТАВ ЗАДАНИЯ

2.1. Определить оценки математического ожидания, дисперсии и средних квадратических отклонений случайных величин Х и Y, заданных в виде двух простых статистических совокупностей  Х^* и  Y^* объемом  n_x = n_y = 20.

          2.2. Проверить правдоподобие гипотезы о принадлежности двух выборок  Х^* и  Y^* единой генеральной совокупности с помощью порядкового критерия Вилькоксона, критериев равенства математических ожиданий и дисперсий двух выборок. Определить уровни значимости, с которыми проверяемая гипотеза не противоречит заданному статистическому материалу.

          2.3. Если гипотеза о принадлежности выборок Х^* и Y^* единой генеральной совокупности Z правдоподобна, то следует определить точечные оценки математического ожидания, дисперсии и среднеквадратического отклонения генеральной совокупности Z на основе объединенной выборки Z^* объемом  n_z = n_y + n_y.

          2.4. Найти интервальные оценки математического ожидания, дисперсии и среднеквадратического отклонения единой генеральной совокупности Z на основе объединенной выборки Z^* при доверительной вероятности Р_Д = 0,95.

          2.5. Проверить гипотезу о нормальности закона распределения, которому подчинена генеральная совокупность Z по критериям Пирсона (c²) и Мизеса (nw²). Определить уровни значимости, с которыми гипотеза о нормальности закона распределения генеральной совокупности Z не противоречит располагаемому статистическому материалу. Построить гистограмму по данным выборки  Z^* и гипотетическую плотность распределения случайной вели-
чины Z.

          2.6. Рассматривая Х^* и  Y^* как выборки случайных величин, входящих в систему, построить корреляционную таблицу, на основе которой определить , а также оценки корреляционного момента  и коэффициента корреляции .

          2.7. Проверить гипотезу об отсутствии корреляционной связи между случайными величинами  X  и  Y  и определить уровень значимости правдоподобия этой гипотезы.

          2.8. Если гипотеза об отсутствии корреляционной связи между величинами X и Y  противоречит располагаемому статистическому материалу, то следует определить доверительный интервал для коэффициента корреляции при доверительной вероятности  Р_Д = 0,95.

          2.9. Определить коэффициенты линейной регрессии  Y^* на  Х^* и оценить с помощью критерия Фишера статистическую значимость полученной регрессии.

          2.10. Составить отчет, содержащий результаты выполнения предыдущих пунктов задания с четкими выводами по каждому пункту.

3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

3.1. Определение статистических оценок числовых характеристик

случайных величин

          Статистические оценки математического ожидания и дисперсии генеральной совокупности Х, удовлетворяющие требованиям состоятельности, несмещенности и эффективности, определяются по выражениям:

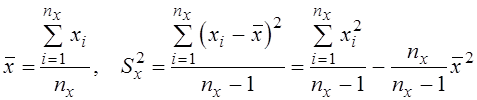                            ,            (3.1)

где n_x  –  объем выборки из генеральной совокупности Х.

          Оценки этих же числовых характеристик для объединенной статис-
тической выборки  Z^* определяются на основе вычисленных значений  для выборок Х^* и  Y^* по выражениям:

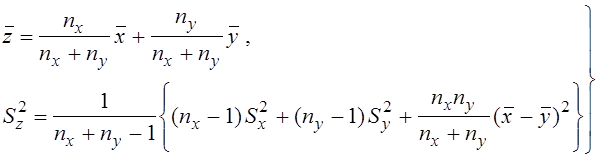     .    (3.2)

          Выражения (3.1) и (3.2) позволяют определить точечные оценки соответствующих числовых характеристик, зависящие от объема выборок. Надежность и точность оценок числовых характеристик повысится, если определять их интервальные оценки, указывая вероятность, с которой интервал изменения оценки накроет истинное значение оцениваемой числовой характеристики. Такие интервалы называются доверительными, указанные же вероятности – доверительными вероятностями Р_Д. В случае достаточного объема выборок доверительные вероятности для оценок математического ожидания и дисперсии связаны с доверительными интервалами при помощи соотношений:

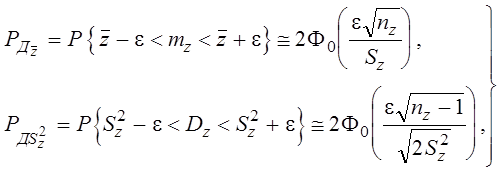                 (3.3)

где 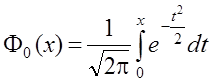 – функция Лапласа.

3.2.Проверка гипотезы о принадлежности двух выборок Х^* и  Y^*