Критерий nw2 основан на рассмотрении отклонений статистической функции распределения для каждого члена выборки z1, z2,…znz от соответствующих значений гипотетической функции распределения. Поэтому этот критерий лишен того недостатка критерия Пирсона, который связан с произвольным разбиением исходной статистической информации на интервалы.
Сама же группировка информации при использовании критерия Пирсона связана с некоторой потерей исходной информации.
За меру отклонения при использовании критерия nw2 принимается следующая величина:
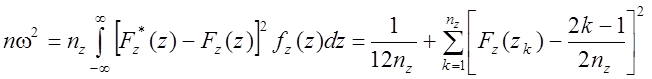 . (3.18)
. (3.18)
Выражение
(3.18) можно использовать, если ![]() известна.
Однако при проверке гипотезы о нормальности закона распределения используются
оценки математического ожидания и дисперсии случайной величины Z, определенной из той же выборки Z*. Поэтому использование
выражения (3.18) для определения меры nw2 – некорректно. Можно предложить следующий способ более
корректного применения критерия nw2 при решении поставленной задачи:
известна.
Однако при проверке гипотезы о нормальности закона распределения используются
оценки математического ожидания и дисперсии случайной величины Z, определенной из той же выборки Z*. Поэтому использование
выражения (3.18) для определения меры nw2 – некорректно. Можно предложить следующий способ более
корректного применения критерия nw2 при решении поставленной задачи:
– оценки
математического ожидания и дисперсии генеральной совокупности определяются на
основе выборки X*: ![]() и
и
![]() ;
;
– эмпирические
функции распределения генеральной совокупности определяются на основе выборки Y*: ![]() и
и ![]() .
.
Тогда
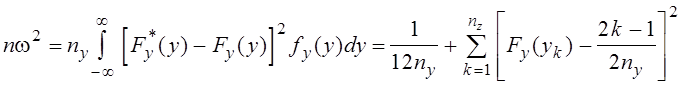 . (3.19)
. (3.19)
При проверке гипотезы о нормальности закона распределения генеральной совокупности Z* выражение (3.19) представляется в виде
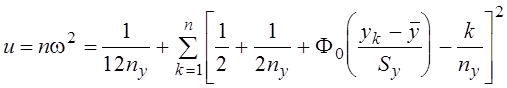 . (3.20)
. (3.20)
Следует
отметить, что реализации Y при использовании
выражения (3.20) должны быть представлены в виде вариационного ряда ![]() .
.
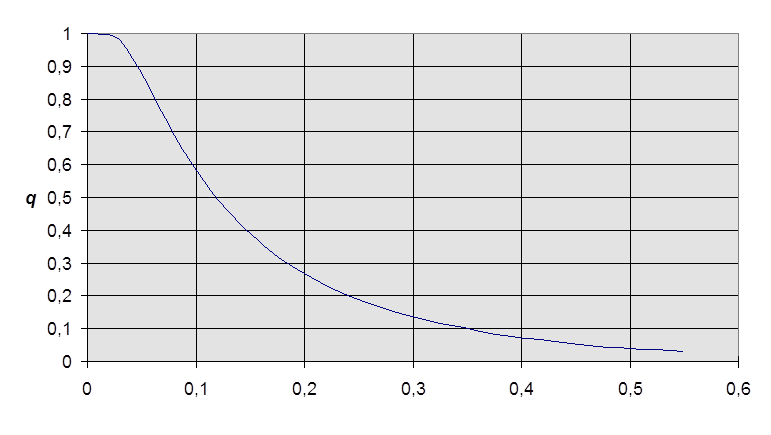
Зависимость уровня значимости правдоподобия гипотезы о виде закона распределения от величины рассчитанного критерия u = nw2 приведена на рис. 3.2.
nw2
Рис. 3.2. Зависимость q от nw2
3.4. Статистика системы случайных величин Х и Y
3.4.1. Точечные оценки числовых характеристик системы
При выполнении этого
пункта задания исходные выборки Х* и Y*
рассматриваются как выборки объема nx = ny = n
из генеральных совокупностей Х и Y, образующих
систему случайных величин. Требуется определить статистические оценки ![]() и статистическую оценку коэффициента корреляции
rxy.
и статистическую оценку коэффициента корреляции
rxy.
Для решения этих задач следует составить корреляционную таблицу, примерный вид которой приводится в табл. 3.2.
Т а б л и ц а 3.2
Корреляционная таблица
|
x y |
x1…x2 |
x2…x3 |
. . . |
xi…xi+1 |
xk…xk+1 |
||
|
|
|
|
|
||||
|
y1…y2 |
|
m11 |
m12 |
m1i |
m1k |
||
|
y2…y3 |
|
m21 |
m22 |
m2i |
m2k |
||
|
. . . |
|||||||
|
yj…yj+1 |
|
mj1 |
mj2 |
mji |
mjk |
||
|
. . . |
|||||||
|
yl…yl+1 |
|
ml1 |
ml2 |
mli |
mlk |
||
Примечания:
1. ![]() и
и ![]() – средние значения величин для
соответствующих интервалов
– средние значения величин для
соответствующих интервалов
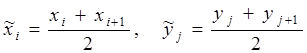 .
.
2. 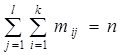 .
.
Введем обозначения: 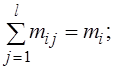
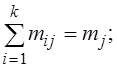
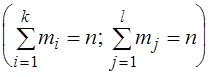 .
.
Тогда числовые характеристики системы Х* и Y* определятся как
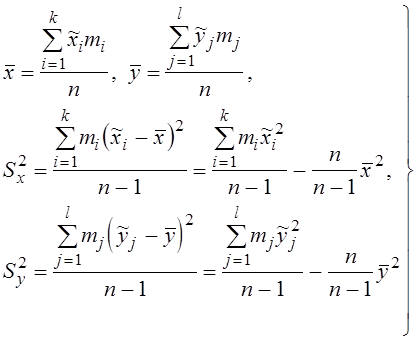 (3.21)
(3.21)
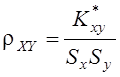 – статистическая оценка коэффициента
корреляции.
– статистическая оценка коэффициента
корреляции.
Статистическая
оценка корреляционного момента ![]() определяется
как
определяется
как
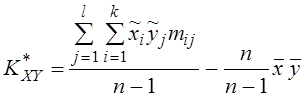 . (3.22)
. (3.22)
3.4.2. Проверка гипотезы об отсутствии корреляционной связи
между случайными величинами X и Y
Если в результате проведенной серии испытаний получено некоторое значение статистического коэффициента корреляции между случайными величинами, отличное от нуля, то это еще не означает, что корреляционная связь действительно существует.
Для оценки уровня значимости правдоподобия гипотезы об отсутствии корреляционной связи перейдем от статистики выборочного значения коэффициента корреляции RXY к статистике Т [2]:
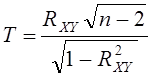 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.