Основы математической статистики: Методические указания к расчетному заданию по курсу "Теория вероятностей и математическая статистика", страница 2

единой генеральной совокупности

3.2.1. Порядковый критерий Вилькоксона [1]

          Поскольку оценки числовых характеристик двух выборок Х^* и Y^* отличаются между собой не настолько, чтобы сразу же было можно утверждать, что генеральные совокупности, из которых получены выборки, разнородны, возникает гипотеза о принадлежности двух выборок единой генеральной совокупности Z. Применим для проверки правдоподобия этой гипотезы три разных критерия: порядковый критерий Вилькоксона, оперирующий всеми значениями выборок Х^* и  Y^*, критерий равенства математических ожиданий (критерий z), оперирующий с оценками математических ожиданий, дисперсий выборок и их объемами, а также  критерий равенства дисперсий (критерий F), оперирующий с дисперсиями и объемами выборок Х^* и  Y^*.

          Для использования критерия Вилькоксона необходимо прежде всего составить единый вариационный ряд для двух выборок  Х^* и  Y^*, т.е.  перемешанный ряд по признаку возрастания элементов выборок. Критерием согласия выдвинутой гипотезы о принадлежности двух выборок единой генеральной совокупности служат числа инверсий  И_x-y и  И_y-x, характеризующие степень перемешанности единого вариационного ряда. Количественная оценка степени перемешанности вариационных рядов дается числом инверсий, которое определяется следующим образом: если какому-либо значению x_k
в объединенной выборке предшествует значение y_i, то  эта пара дает одну инверсию иксов с игреками.

          Покажем на примере, как определяются числа инверсий. Пусть, например, имеется единый вариационный ряд

                                                  x₁ y₁ x₂ x₃ y₂ x₄ y₃ y₄ x₅.

Этот ряд дает следующие числа инверсий:

                              И_Y-X = 1 + 3 + 4 + 4 = 12, И_X-Y = 1 + 1 + 2 + 4 = 8,

причем .

          Вилькоксон показал, что числа инверсий И_x-y è И_y-x подчинены нормальному закону с параметрами:

                                        ,

                              .

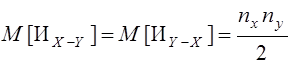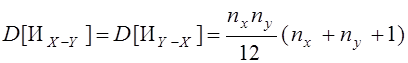          Поскольку порядковый критерий Вилькоксона является двусторонним критерием (критическая область значений критерия содержит две подобласти И < И_кр1  и  И > И_кр2), уровень значимости, с которым гипотеза об объединяемости выборок в единую генеральную совокупность не противоречит располагаемому статистическому материалу, определяется как

q =1 - Р(И(Y-X) набл < И < И(X-Y)набл) =

=

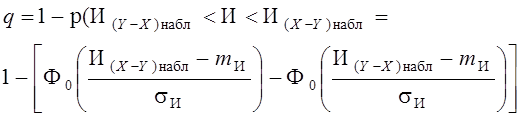                           (3.4)

Так как 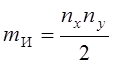, а , то выражение (3.4) запишется в виде

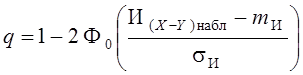.                                 (3.5)

(В выражениях (3.4) и (3.5) предполагается, что , а   .)

3.2.2.  Критерий равенства математических ожиданий

          Зачастую исследователь располагает не всеми реализациями двух выборок  Х^* и  Y^*, а лишь объемами этих выборок  n_x, n_y  и статистическими оценками их математических ожиданий () и дисперсий (). В этом случае для оценки правдоподобия гипотезы о принадлежности двух выборок единой генеральной совокупности можно воспользоваться критерием равенства математических ожиданий двух независимых выборок – критерием  Z:

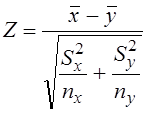                                                   .                                           (3.6)

          Случайная величина 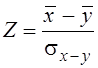 при справедливости выдвинутой гипотезы распределена по нормальному закону с параметрами m_z = 0; D_z = s_z = 1. Следовательно, поскольку критерий Z – двусторонний, уровень значимости гипотезы о принадлежности двух независимых выборок единой генеральной совокупности при наблюденном значении критерия z_набл определится как

                                                  q = 1 – 2 Ф₀ (z_набл),                                        (3.7)

где   z_набл > 0.

3.2.3. Критерий равенства дисперсий (Р. Фишера) [2]

          При использовании критерия равенства дисперсий двух независимых выборок задача заключается в проверке, является ли значимым различие в оценках дисперсий двух выборок  Х^* и  Y^*. В качестве критерия проверки используется в этом случае статистика Фишера:

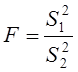                                                            ,                                               (3.8)