Определение статистических оценок математического ожидания и дисперсии двух выборок

Расчетное задание «Основы математической статистики».

Студент: Ручкин Н.В.

Группа: ЭН 2-81

ВАРИАНТ № 15  

Состав задания:   Заданы две независимые выборки случайных чисел, распределенных по  нормальным законам.

Выборки:

№8	№10
344	3904
299	3283
311	3211
298	3021
321	3297
303	3083
295	2676
332	3084
334	3782
331	3811
354	3668
300	3199
303	3220
325	3254
313	3249
351	3618
318	3648
326	3637
341	3496
309	3241
316	3288
287	3140
310	3206
273	3113
318	3230
273	3118
298	3077
287	2436
298	2468
295	2482

1. Определить статистические оценки математического ожидания и дисперсии двух выборок.

РЕШЕНИЕ

Для первой выборки:

Число элементов в первой выборке

Рассчитаем выборочное среднее:

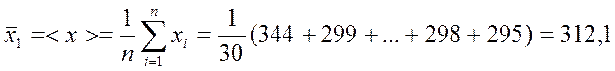
Рассчитаем средний квадрат:

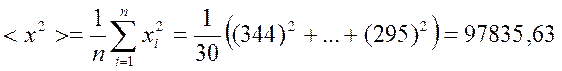
Выборочная дисперсия по формуле:

Выборочное среднеквадратичное стандартное отклонение

Исправленная дисперсия

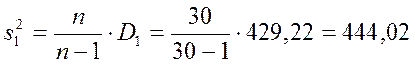
Исправленное среднеквадратичное стандартное отклонение

Для второй выборки:

Число элементов во второй  выборке

Рассчитаем выборочное среднее:

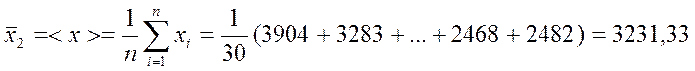
Рассчитаем средний квадрат: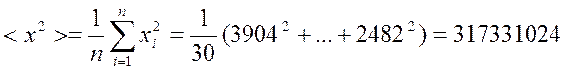

Выборочная дисперсия по формуле:

Выборочное среднеквадратичное стандартное отклонение

Исправленная дисперсия

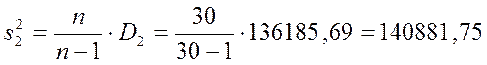
Исправленное среднеквадратичное стандартное отклонение

.

2. Проверить правдоподобие  гипотезы о принадлежности двух выборок единой генеральной совокупности с помощью трех критериев: порядкового критерия Вилкоксона, равенства математических ожиданий и равенства дисперсий (критерий Фишера).

РЕШЕНИЕ

Порядковый критерий Вилкоксона.

Так как объем выборок превышает 25, применим критерий Вилкоксона для больших выборок.

Объем первой выборки

Объем второй выборки

Расположим варианты в виде одного вариационного рядя и перенумеруем их:

Число	Номер	Выборка	Число	Номер	Выборка	Число	Номер	Выборка
273	1	1-ая	321	21	1-ая	3140	41	2-ая
273	2	1-ая	325	22	1-ая	3199	42	2-ая
287	3	1-ая	326	23	1-ая	3206	43	2-ая
287	4	1-ая	331	24	1-ая	3211	44	2-ая
295	5	1-ая	332	25	1-ая	3220	45	2-ая
295	6	1-ая	334	26	1-ая	3230	46	2-ая
298	7	1-ая	341	27	1-ая	3241	47	2-ая
298	8	1-ая	344	28	1-ая	3249	48	2-ая
298	9	1-ая	351	29	1-ая	3254	49	2-ая
299	10	1-ая	354	30	1-ая	3283	50	2-ая
300	11	1-ая	2436	31	2-ая	3288	51	2-ая
303	12	1-ая	2468	32	2-ая	3297	52	2-ая
303	13	1-ая	2482	33	2-ая	3496	53	2-ая
309	14	1-ая	2676	34	2-ая	3618	54	2-ая
310	15	1-ая	3021	35	2-ая	3637	55	2-ая
311	16	1-ая	3077	36	2-ая	3648	56	2-ая
313	17	1-ая	3083	37	2-ая	3668	57	2-ая
316	18	1-ая	3084	38	2-ая	3782	58	2-ая
318	19	1-ая	3113	39	2-ая	3811	59	2-ая
318	20	1-ая	3118	40	2-ая	3904	60	2-ая

Сумма порядковых номеров вариант первой выборки

W = 1+2+3+4+…+29+30=210

При  уровне значимости α = 2*Q= 0.05

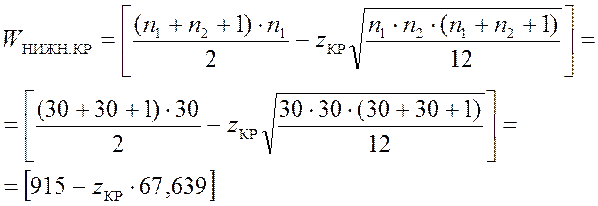
Где Z_КР находим по таблице: Ф(Z_КР)=(1- α)/2

В случае α = 2*Q= 0.05 имеем:

Ф(Z_КР)=(1- α)/2=0,475  и Z_КР =1,96

Тогда

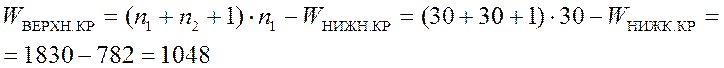
Так как у нас наблюдаемое значение критерия равно 210 и он меньше нижней границы, равной 782, то считать, что случайные величины, выборки из которых представлены имеют общее распределение. Итак – распределения не одинаковы.