Определение статистических оценок математического ожидания и дисперсии двух выборок, страница 2

Вычислим значение параметра T (критерий Стьюдента):

      

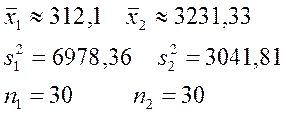
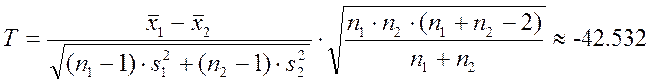
Число степеней свободы

Так как  значение критерия  , то гипотеза об однородности выборок отвергается.

Критерий Фишера

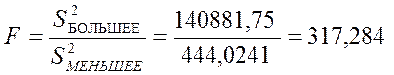
По таблице находим (для больших n интерполируем), что F(α, n, m) =  F(0.05, 30, 30) <2.0

Так как у нас F  >  F(α, n, m)  по этому критерию гипотезу равенства отвергается.

Дисперсии не равны.

3. Если гипотеза о принадлежности двух выборок единой генеральной совокупности не противоречит  располагаемому статистическому материалу, то объединить выборки и определить точечные оценки математического ожидания и дисперсии для объединенной выборки.).

РЕШЕНИЕ.

Располагаемый статистический материал противоречит гипотезе о принадлежности двух выборок единой генеральной совокупности если принять уровень значимости 0,05.

Однако с какой-то очень маленькой вероятностью, эти выборки все же могут принадлежать одной генеральной совокупности. Такой уровень значимости всегда найдется. Считаем далее, что эти выборки принадлежат одной генеральной совокупности.

Объединим выборки и рассчитаем:

Общее число элементов в объединенной выборке:

Выборочное среднее

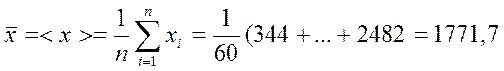
Средний квадрат величины в выборке: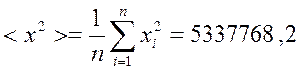

Выборочная дисперсия:

Выборочное среднеквадратичное стандартное отклонение

Исправленная дисперсия

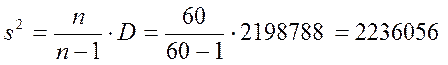
Исправленное среднеквадратичное стандартное отклонение

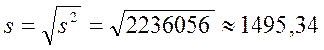
Значит, наилучшие оценки математического ожидания и дисперсии:

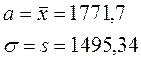
ОТВЕТ:

Наилучшие оценки математического ожидания и дисперсии:

 

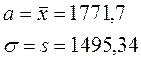
4. Найти интервальные оценки при доверительной вероятности β=0.95 для  статистических оценок МО и дисперсии  объединенной выборки.

РЕШЕНИЕ.

Интервал для оценки математического ожидания имеет вид

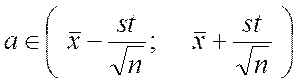
Где

 

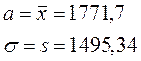
t – значение аргумента функции F (t) такое, что

F (t) =  β / 2 = 0.95 /2=0,475.

По таблице находим t=1,96

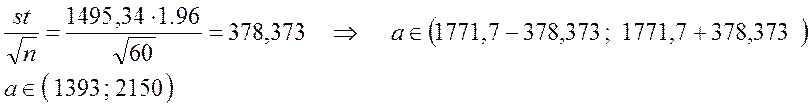
Для оценки σ по таблице 4 найдем для заданного уровня β=0.95 при n =30 значение q=0.28

ОТВЕТ:

С вероятностью β=0.95 математическое ожидание и дисперсия

5. Проверить гипотезу о нормальности закона распределения объединенной выборки по критерию Пирсона, приняв число интервалов k = 6.

РЕШЕНИЕ

Число интервалов равно k=6, тогда длина интервала для группировки

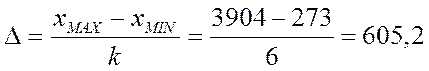
Вычислим  теоретические значения частот и фактические значения частот.

 Для вычисления Ф(x) по таблице найдем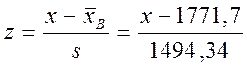

В последнем столбце посчитано количество значений, которые попадают в указанные в начале интервалы.

№	Границы исходных интервалов		Границы нормированных интервалов		Ф(Zi)	Ф(Zi+1)	Pi+1=Ф(Zi+1)-Ф(Zi)	n’=  n* pi+1	n, факт
	Xi	Xi+1	Zi	Zi+1
1	−∞	273	−∞	-1,002516	-0,5	-0,3413	0,1587	4,761	0
2	273	878,166	-1,00252	-0,597544	-0,341	-0,2257	0,1156	3,468	30
3	878,166	1483,33	-0,59754	-0,192573	-0,225	-0,0793	0,1464	4,392	0
4	1483,33	2088,5	-0,19257	0,212401	-0,079	0,0832	0,1625	4,875	0
5	2088,5	2693,66	0,212401	0,617374	0,083	0,2324	0,1492	4,476	4
6	2693,66	3298,83	0,617374	1,022346	0,232	0,3461	0,1137	3,411	18
7	3298,83	3904	1,022347	1,427319	0,346	0,4236	0,0775	2,325	8
8	3904	∞	1,427319	∞	0,423	0,5	0,0764	2,292	0