Определение статистических оценок математического ожидания и дисперсии двух выборок, страница 4

Коэффициент корреляции вычислим по формуле:

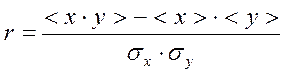
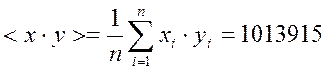
Вычислим

Для оценки значимости этого коэффициента вычислим:

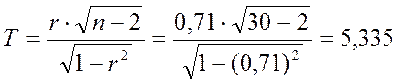
При уровне значимости 0.05 и числе степеней свободы k=n-2=30-2=28 находим по таблице критическое значение распределения Стьюдента равное 2,04

Так как Наблюдаемое значение критерия 5,335 больше критического значения 2,04 то коэффициент корреляции является значимым, то есть существенно отличается от нуля.

Коэффициент корреляции не равен нулю.

ОТВЕТ:

Коэффициент корреляции не является значимым по критерию Стьюдента с уровне значимости 0.05. Следовательно, выборки независимы.

8. Построить 2 линии регрессии:   Y на X   и    X  на  Y.

РЕШЕНИЕ:

Уравнения регрессии имеют вид:

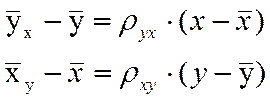
Где коэффициенты

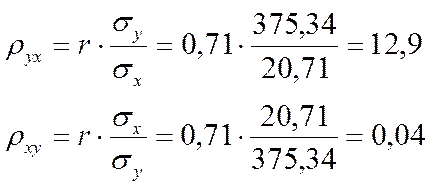
Получим уравнения регрессии:

Регрессия Y по X:

y(x)=-784,8 +12,9x

Регрессия  X по Y:

x(y)= 186.1+0,04y

Для построения линий регрессии вычислим значения в 2-х точках для каждой прямой

x	y( Регрессия Y по X)	y (Регрессия X по Y)
273	2737	2172
354	3782	4197

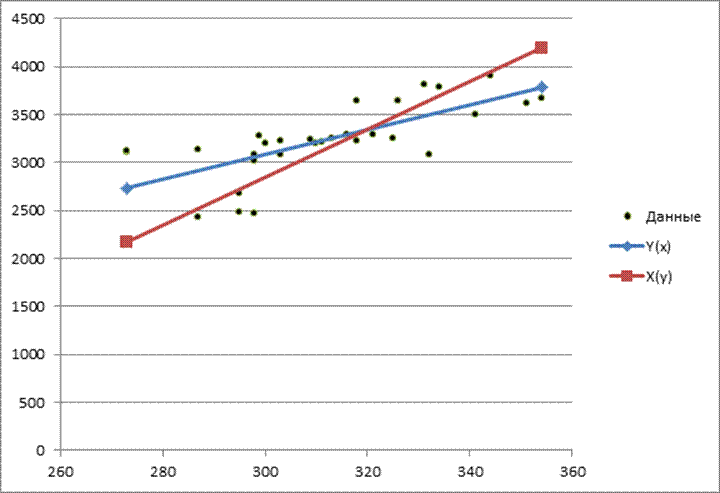
ОТВЕТ:

Данные коррелированны, коэффициент линейной корреляции равен 0,71.

Линии регрессии пересекаются в точке с координатами  средних значений (примерно). 

9. Составить пояснительную записку к выполненному расчетному заданию с четкими выводами по каждому из  его пунктов.

1) Выборочное среднее является наилучшей несмещенной оценкой математического ожидания, а исправленная дисперсия и исправленное средне квадратичное отклонение являются наилучшими несмещенными оценками для генерального по каждой из выборок.

2) Критерий Вилкоксона, Стьюдента и Фишера показал неравенство средних и дисперсий. Нельзя считать (при уровне достоверности 0.05) что обе выборки описываются одним и тем же нормальным распределением.

3) Наилучшие оценки математического ожидания и дисперсии:

 

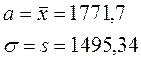
4) Найдены интервальные оценки при доверительной вероятности β=0.95 для  статистических оценок МО и дисперсии  объединенной выборки.

5) Проверка гипотезы о нормальности закона распределения объединенной выборки по критерию Пирсона при 6 интервалах показала, что распределение не совпадает с нормальным (с уровнем значимости 0,05).

6) График теоретического распределения и фактическая гистограмма не близки друг к другу, это лишний раз свидетельствует о том, что закон распределения объединенной выборки  далек от нормального.

7) Коэффициент корреляции не является значимым по критерию Стьюдента с уровне значимости 0.05. Из этого следует, что выборки независимы.

8) Данные коррелированны, коэффициент линейной корреляции равен 0,71.

Линии регрессии пересекаются близко к точке с координатами  средних значений.