Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
ли ![]() . Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим:
. Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() . Возведём ещё раз в квадрат:
. Возведём ещё раз в квадрат: ![]() Или
Или ![]()
 Поделив всё равенство на
правую часть, получим каноническое уравнение эллипса с фокусами на
действительной оси:
Поделив всё равенство на
правую часть, получим каноническое уравнение эллипса с фокусами на
действительной оси: 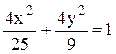 .
.
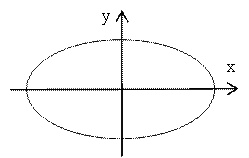
Ответ. Данное соотношение представляет уравнение эллипса 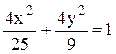 .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
 Или
Или ![]() . Перенесём второй корень в правую часть неравенства и
возведём обе части в квадрат. Получим:
. Перенесём второй корень в правую часть неравенства и
возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() . Отметим, что при 1+8x>0 данное
неравенство выполняется всегда. Поэтому границу области, определяемой неравенством,
нужно искать при 1+8x<0, т.е. x<-1/8. Возведём полученное
равенство ещё раз в квадрат:
. Отметим, что при 1+8x>0 данное
неравенство выполняется всегда. Поэтому границу области, определяемой неравенством,
нужно искать при 1+8x<0, т.е. x<-1/8. Возведём полученное
равенство ещё раз в квадрат: ![]() Или
Или ![]() Поделив всё равенство на правую часть,
получим :
Поделив всё равенство на правую часть,
получим : 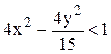 .
.
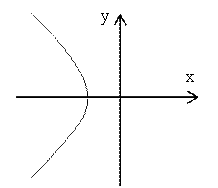
Ответ. Данное соотношение представляет область, являющуюся
внешней часть левой ветви гиперболы 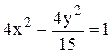 ( так как переменная x на
границе области должна быть отрицательной).
( так как переменная x на
границе области должна быть отрицательной).
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Возведём обе части в квадрат. Получим:
. Возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() Уравнение
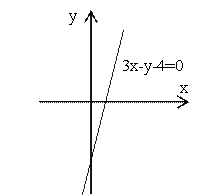
можно поделить на 2, получим: 3x-y-4=0.
Уравнение
можно поделить на 2, получим: 3x-y-4=0.
Ответ. Данное соотношение представляет уравнение прямой ![]() .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
 Или
Или ![]() . Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим:
. Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() . Возведём ещё раз в квадрат:
. Возведём ещё раз в квадрат: ![]() Или
Или ![]()
Поделив всё равенство на
правую часть, получим каноническое уравнение эллипса с фокусами на мнимой оси: 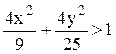 .
.
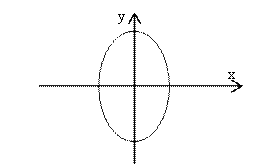
Ответ. Данное соотношение представляет внешнюю часть
эллипса: 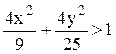 .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Возведём обе части в квадрат. Получим:
. Возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() Уравнение
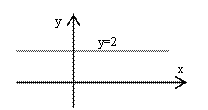
можно поделить на 2, получим: y=2.
Уравнение
можно поделить на 2, получим: y=2.
Ответ. Данное соотношение представляет уравнение прямой ![]() .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Возведём обе части в квадрат. Получим:
. Возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]()
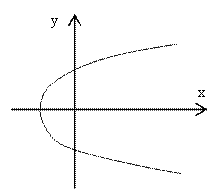
Ответ. Данное соотношение представляет область,
расположенную внутри параболы ![]() с вершиной в точке
(-1/2; 0)
с вершиной в точке
(-1/2; 0)
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Возведём обе части в квадрат. Получим:
. Возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]()
Ответ. Данное соотношение представляет область,
расположенную внутри параболы ![]() с вершиной в точке
(1/2; 0)
с вершиной в точке
(1/2; 0)
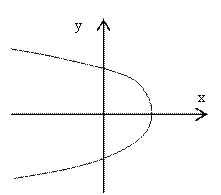
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: 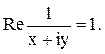
Или 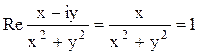 . Приравнивая числитель и знаменатель, получим:
. Приравнивая числитель и знаменатель, получим: ![]() . Выделяя полный квадрат разности, можно
записать:
. Выделяя полный квадрат разности, можно
записать: ![]()
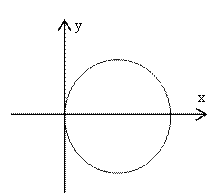
Ответ. Данное соотношение представляет окружность радиуса 1/2 с центром в точке (1/2; 0)
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Из этого следует, что
. Из этого следует, что ![]() . Левое неравенство означает, что
. Левое неравенство означает, что
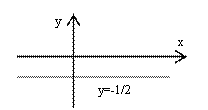 y<0, а правое – что y>-1/2. Объединяя последние
неравенства, можно записать:
y<0, а правое – что y>-1/2. Объединяя последние
неравенства, можно записать: ![]()
Ответ. Данное соотношение определяет область, заключённую
между прямыми y=0 и ![]() .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: 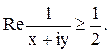
Или 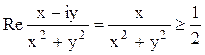 . Приводя к общему знаменателю и отбрасывая его,
получим:
. Приводя к общему знаменателю и отбрасывая его,
получим: ![]() . Выделяя полный квадрат разности, можно
записать:
. Выделяя полный квадрат разности, можно
записать: ![]()
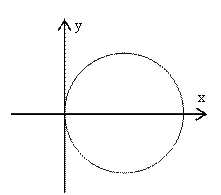
Ответ. Данное соотношение представляет круг радиуса 1 с центром в точке (1; 0)
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
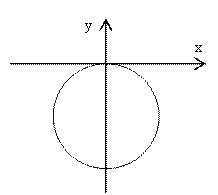
![]()
 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: 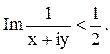
Или 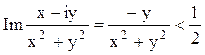 . Приводя к общему знаменателю и отбрасывая его,
получим:
. Приводя к общему знаменателю и отбрасывая его,
получим: ![]() . Выделяя полный квадрат суммы, можно
записать:
. Выделяя полный квадрат суммы, можно
записать: ![]()
Ответ. Данное соотношение определяет область, расположенную вне круга радиуса 1 с центром в точке (0;-1).
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
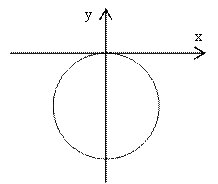
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: 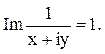
 Или
Или 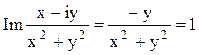 . Приводя к общему знаменателю и отбрасывая его,
получим:
. Приводя к общему знаменателю и отбрасывая его,
получим: ![]() . Выделяя полный квадрат суммы, можно
записать:
. Выделяя полный квадрат суммы, можно
записать: ![]()
Ответ. Данное соотношение представляет окружность радиуса 1/2 с центром в точке (0; -1/2)
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
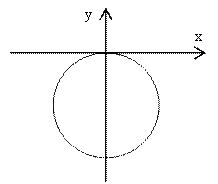 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: 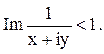
Или 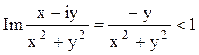 . Приводя к общему знаменателю и отбрасывая его,
получим:
. Приводя к общему знаменателю и отбрасывая его,
получим: ![]() . Выделяя полный квадрат суммы, можно
записать:
. Выделяя полный квадрат суммы, можно
записать: ![]()
Ответ. Данное соотношение определяет область, расположенную вне круга радиуса 1/2 с центром в точке (0; -1/2).
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Перенесём второй корень в правую часть равенства
. Перенесём второй корень в правую часть равенства
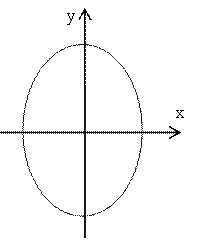 и возведём обе части в
квадрат. Получим:
и возведём обе части в
квадрат. Получим: ![]() . Или
. Или ![]() .
Возведём ещё раз в квадрат:
.
Возведём ещё раз в квадрат: ![]() Или
Или ![]()
Поделив всё равенство на
правую часть, получим каноническое уравнение эллипса с фокусами на мнимой оси: 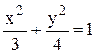 .
.
Ответ. Данное соотношение представляет уравнение эллипса 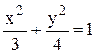 .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
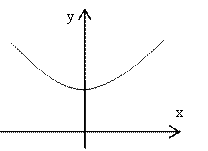
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим:
. Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() . Заметим, что правая часть не должна быть
отрицательной, т.е. y>1/4. Возведём ещё раз в квадрат:
. Заметим, что правая часть не должна быть
отрицательной, т.е. y>1/4. Возведём ещё раз в квадрат: ![]() Или
Или ![]()
Поделив всё равенство на
правую часть, получим каноническое уравнение гиперболы с фокусами на мнимой
оси: 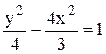 .
.
Ответ. Данное соотношение определяет верхнюю ветвь гиперболы
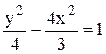 .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
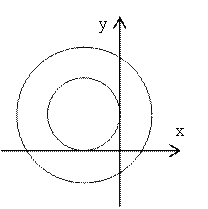 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Возведём все части неравенства в квадрат. Получим:
. Возведём все части неравенства в квадрат. Получим: ![]() Это неравенство определяет кольцо,
заключённое между окружностью
Это неравенство определяет кольцо,
заключённое между окружностью ![]() радиуса 1 с центром в
точке (-1;1) и окружностью
радиуса 1 с центром в
точке (-1;1) и окружностью ![]() радиуса 2 с центром в
той же точке.
радиуса 2 с центром в
той же точке.
Ответ. Данное соотношение определяет кольцо![]()
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Возведём обе части неравенства в квадрат. Получим:
. Возведём обе части неравенства в квадрат. Получим: ![]() Или
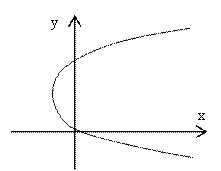
Или ![]() Это
неравенство определяет параболу с фокусом на оси ОХ с вершиной в точке (-1/2; 1
Это
неравенство определяет параболу с фокусом на оси ОХ с вершиной в точке (-1/2; 1
Ответ. Данное соотношение определяет параболу
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Возведём все части неравенства в квадрат. Получим:
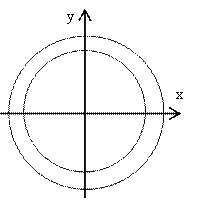
. Возведём все части неравенства в квадрат. Получим: ![]() Это неравенство определяет кольцо,
заключённое между окружностью
Это неравенство определяет кольцо,
заключённое между окружностью ![]() радиуса 3 с центром в
точке (0;1) и окружностью
радиуса 3 с центром в
точке (0;1) и окружностью ![]() радиуса 4 с центром в
той же точке.
радиуса 4 с центром в
той же точке.
Ответ. Данное соотношение определяет кольцо ![]()
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
 Или
Или ![]() . Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим:
. Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() . Заметим, что правая часть не должна быть
отрицательной, т.е. y>1/8. Возведём ещё раз в квадрат:
. Заметим, что правая часть не должна быть
отрицательной, т.е. y>1/8. Возведём ещё раз в квадрат: ![]() Или
Или ![]()
Поделив всё равенство на
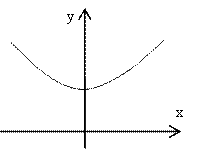
правую часть, получим каноническое уравнение гиперболы с фокусами на мнимой
оси: 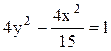 .
.
Ответ. Данное соотношение определяет верхнюю ветвь гиперболы
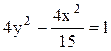 .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим:
. Перенесём второй корень в правую часть равенства и
возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() . Отметим, что правая часть равенства не
должна быть отрицательной, т.е. должно быть 4+8y<0, y<-1/2.
Возведём полученное равенство ещё раз в квадрат:
. Отметим, что правая часть равенства не
должна быть отрицательной, т.е. должно быть 4+8y<0, y<-1/2.
Возведём полученное равенство ещё раз в квадрат: ![]() Или
Или ![]()
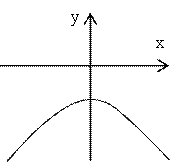 Поделив всё равенство на
правую часть, получим каноническое уравнение гиперболы с фокусами на мнимой
оси:
Поделив всё равенство на
правую часть, получим каноническое уравнение гиперболы с фокусами на мнимой
оси: 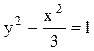 .
.
Ответ. Данное соотношение представляет уравнение нижней
ветви гиперболы 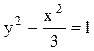 ( так как переменная y должна
быть отрицательной).
( так как переменная y должна
быть отрицательной).
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Перенесём второй корень в правую часть неравенства и
возведём обе части в квадрат. Получим:
. Перенесём второй корень в правую часть неравенства и
возведём обе части в квадрат. Получим: ![]() . Или
. Или ![]() . Отметим, что правая часть неравенства не
может быть отрицательной. Тогда 36+20x<0, т.е. x<-36/20=-9/5.
Возведём полученное равенство ещё раз в квадрат:
. Отметим, что правая часть неравенства не
может быть отрицательной. Тогда 36+20x<0, т.е. x<-36/20=-9/5.
Возведём полученное равенство ещё раз в квадрат: ![]() Или
Или ![]() Поделив всё равенство на правую часть,
получим :
Поделив всё равенство на правую часть,
получим : 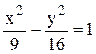 .
.
Ответ. Данное соотношение представляет левую ветвь
гиперболы 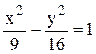 .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
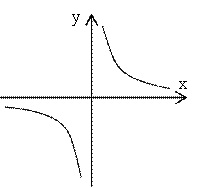
Или ![]() . Это уравнение гиперболы, ветви которой расположены в
первой и третьей четвертях координатной плоскости:
. Это уравнение гиперболы, ветви которой расположены в
первой и третьей четвертях координатной плоскости: ![]() .
.
Ответ. Данное соотношение представляет гиперболы ![]() .
.
Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж.
![]()
 Решение. Так как z=x+iy, то данное соотношение имеет вид:
Решение. Так как z=x+iy, то данное соотношение имеет вид: ![]()
Или ![]() . Это уравнение гиперболы, фокусы которой расположены
. Это уравнение гиперболы, фокусы которой расположены
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.