Действия с комплексными числами. Различные формы представления комплексного числа

Деиствия с к.ч. модуль к.ч. Разл.формы представления к. числа

Комплексными числами (к.ч.) называются пары () действительных чисел  и , если для них определены понятия равенства и операции сложения и умножения следующим образом:

1. Два к.ч. () и () равны , .

2. Суммой двух к.ч. () и () называется к.ч. () .

3. Произведением к.ч. () и () называется к.ч. ()

Каждое к.ч. () принято обозначать символом  и оно представимо в алгебраической форме: . Число  называется действительной частью к.ч. , обозначается Re; число  называется мнимой частью к.ч. , обозначается символом . Величина 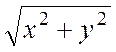 называется модулем к.ч. , обозначается символом : =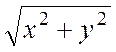. Любое число , удовлетворяющее равенствам 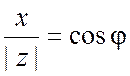, , 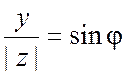называется аргументом к.ч. , обозначается символом . Аргумент определен для z¹0 лишь с точностью до любого слагаемого, кратного 2p, то есть j=argz+2kp, kÎZ. Для однозначных функций 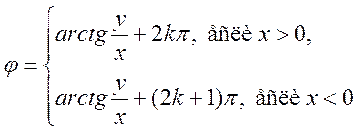, kÎZ и arctg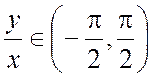. Тригонометрической формой к.ч. называется его запись в виде . В показательной форме к.ч.  имеет вид  или , где = (формула Эйлера).

К. ч.  называется сопряженным с к.ч. , обозначается символом : , если .

Функции к. п.: опр, усл. Коши-Римана дифференцируемости функции в т., геом. смысл производной. Дифференцируемые функции. Условия Коши — Римана

DEF Ф-ия f наз. регулярной в нек. точке z₀, если в нек. окрестности этой точки она представима в виде сходящегося степенного ряда f(z) = å _n^¥₌₁C_n(z – z₀) ⁿ. DEF Пусть функция f(z) опред. в нек. окрестности точки z₀. Если сущ. конечный предел отно­шения (f(z₀+Dz)-f(z₀))/Dz при Dz® 0, то этот предел наз. производной функции f(z) в точке z₀ и обозначается f '(z₀), а ф-ия f(z) наз. дифференцируемой в точке z₀. Таким образом, f’(z₀) = lim_{Dz® 0}(f(z₀+Dz)-f(z₀))/Dz  (1) DEF Ф-ия f(z) наз. дифф-мой в обл-ти, если она дифф-ма в каждой точке этой обл-ти. Пусть Df = f(z₀+Dz) - f(z₀). Тогда соотношение (1) примет вид lim_{Dz® 0}Df /Dz =f ’(z₀)  (2). Это означает, что для любого e >0 существует d =d(e)>0 та­кое, что неравенство  |Df /Dz - f ’(z₀)| < e имеет место, если 0<½Dz½<d. Из (2) следует, что  Df = f ‘(z₀)Dz + o(Dz) (Dz®0). Обратно, если приращение Df функции f(z) представляется в виде Df =A Dz + +o(Dz) (3),где A — комплексная постоянная, не зависящая от Dz, то функ­ция f(z) дифференцируема в точке z₀ и A = f ‘(z₀). Таким образом, равенство (3) является необходимым и до­статочным условием дифференцируемости функции f(z) в точке z₀ .Из определения производной и свойств пределов вытекает, что на функции комплексного переменного распространяются правила дифферен­цирования. 1. Если функции f(z) и g(z) дифференцируемы в точке z, то их сумма, разность, произведение и частное (при g(z)¹0) так­же дифференцируемы в этой точке и имеют место равенства (f± g)' = f ’± g'; (cf)' = cf ’   (с = const), (fg)’ = f ’g + fg’ , (f/g)’ = (f ‘g – fg’)/g²  (6)    2. Если функция f(z) дифференцируема в точке z, а функ­ция F(w) дифференцируема в точке w=f(z), то функция Ф(z)=F[f(z)] дифференцируема в точке z, причем Ф^r(z)=F'(w)f'(z}. (7)

2. Условия Коши — Римана. Теорема1. Для того чтобы ф-ия f(z)=u(x, y}+ iv{x, у) была дифференцируема в точке z=x+iy, необходи­мо и достаточно, чтобы

1) функции и{х, у} и v(x, у) были дифференцируемы, в точ­ке (х, у);

2) в точке (х, у) выполнялись условия Коши – Римана : ¶u/¶x = ¶v/¶y, ¶u/¶y = - ¶v/¶x (8) Для производной f ‘(z) справедлива формула f ‘(z) = ¶u/¶x+ i¶v/¶x = ¶v/¶y -i¶u/¶y (9)

Док.Необходимость.Пусть ф-ия f(z) дифференцируема в т. z. Тогда в силу (3) имеем Df =f ‘(z)Dz + e(r) (10), где в e(r)=о(r) при r®0. Здесь обозначено r = |Dz| = ((Dx)² + (Dy)²)^1/2. Функция e(r) комплекснозначная, представим ее в виде e(r)=e₁(r)+ie₂(r), где функции e₁(r), e₂(r) прини­мают действительные значения. Так как e(r)/r ®0 при r®0, то e₁(r)/r ®0, e₂(r)/r ®0 при r®0 , и поэтому e₁(r)=о(r), e₂(r)=о(r) (r®0). (11) Обозначим  Df = Du+iDv,   f ‘(z)==A+iB и подставим в (10), тогда получим Du+iDv = (A+iB)(Dx+iDy)+e₁+ie₂  (12) Приравнивая в этом соотношении действительные и мнимые ча­сти, получаем Du = ADx - BDy + e₁ Dv = BDx + ADy + e₂. (13) Тем самым доказано, что функции и, v дифференцируемы в точ­ке (х, у).Из равенств (13) находим A =¶u/¶x  , -B = ¶u/¶y , B = ¶v/¶x, A = ¶v/¶y , откуда следуют условия Коши-Римана и формула (9), так как f(z}=A+iB. Достаточность. Пусть функции u(х, у) и v(х, у) диф­ференцируемы в точке (х, у) и пусть выполняются условия (8). Тогда имеют место равенства (13), где e₁(r)=о(r), e₂(r)=о(r). Ум­ножая второе из этих равенств на i и складывая с 1-ым, получаем Du+ iDv=  =ADx - BDy + i(BDx + ADy)+e₁+e₂ , или Df = (A+iB)(Dx+ iDy)+e₁+ie₂или Df = =(A+iB)Dz+e(r), где e(r)=о(r), откуда в силу (3) вытекает дифференцируемость функции f(z) в точке z.