РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА.
Содержание работы.
1. Построить точечные множества на плоскости, определяемые заданными условиями.
2. Построить образы множеств G при заданном отображении w=f(z).
3. Найти область однолистности указанной функции, построить эту область и образ области однолистности.
4. Выделить регулярную ветвь однолистной функции, построить для нее область однолистности и вычислить значение функции в заданной точке z0.
5. Разложить в ряд Лорана функцию f(z) либо в окрестности указанной точки, либо в указанной области.
6. Вычислить интегралы.
7. Вычислить несобственные интегралы.
Варианты.
1. 1.Im z £1; 0
<|z+1+i| £1; 0£ arg z £ ![]() ; | z- i| - | z - i|<1; |
z-1|=|Re z|.
; | z- i| - | z - i|<1; |
z-1|=|Re z|.
2. 0< Re z<3; 1£ | z | <3; ![]() £ arg z £
£ arg z £ ![]() ; | z+i |+| z+1-i
| ³3; Re
; | z+i |+| z+1-i
| ³3; Re![]() >
>![]() .
.
3. 0< Re z+Im z<1; 2<|
z-i | £3; 0<arg z< ![]() ;
;
| z+i| - | z+1+i|<3; Re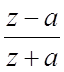 =0, a>0.
=0, a>0.
4. -1£Re z<1; 1<| z |£ 2; ![]() £ arg z £
£ arg z £ ![]() ; | z-i|+|z|£ 2; |
z|>1-Re z.
; | z-i|+|z|£ 2; |
z|>1-Re z.
5. -1< Re z - Im z £0; 1<|
z-1+i | £ 2; ![]() <arg z £
<arg z £![]() ;
;
| z | - | z+i|>2; Re(z
(1-i))<![]() .
.
2. 1. G : Re z ³1; w=z2;
G : { | z |£1, Im z>0}, w=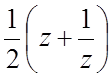 ;
;
G : 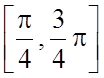 , w=
, w=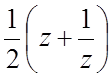 ;
;
G : { -1£Re z<0, |Im z|£ p}, w=![]() .
.
2. G : Im z£1; w=z2;
G : { | z | ³1, Im z<0}, w=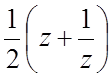 ;
;
G : 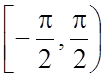 , w=
, w=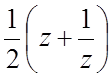 ;
;
G : { 0 £Re z £1, |Im z|£ p}, w=![]() .
.
3. G : Re z£ -1; w=z2;
G : { | z |£1, Re z>0}, w=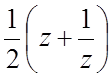 ;
;
G :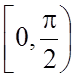 , w=
, w=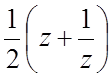 ;
;
G : { 0 £Re z <1, 0£ Im z £ 2p}, w=![]() .
.
4. G : Im z£ -1; w=z2;
G : { | z | ³1, Re z<0}, w=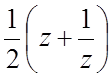 ;
;
G :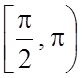 , w=
, w=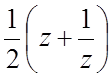 ;
;
G : { Re z >1, 0£ Im z £ 2p}, w=![]() .
.
3. 1. w=sin z;
2. w= tg z;
3. w= ctg z;
4. w= th z;
5. w= sh z;
6. w= ch z;
7. w= cth z.
4. 1. f(z)=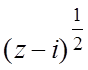 , f( 2i)=
, f( 2i)=![]() +i
+i![]() , z0=0;
, z0=0;
f(z)=Ln(1- z), f( 0)=2p i, z0=2;
2. f(z)=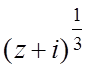 , f( 0)=
, f( 0)=![]()
![]() , z0=
-1+i;
, z0=
-1+i;
f(z)=Ln(1+ z), f( -2)=3p i, z0=i;
3. f(z)=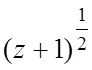 , f( -2)=
-i, z0=2-i;
, f( -2)=
-i, z0=2-i;
f(z)=Ln( z-i ), f( 1)=![]() ln2+ i
ln2+ i![]() , z0=0;
, z0=0;
4. f(z)=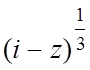 , f( -1+i)=
, f( -1+i)=![]() +i
+i![]() , z0= 2i;
, z0= 2i;
f(z)=Ln(z+i), f( 1)=![]() ln2+ i
ln2+ i![]() , z0=
-1.
, z0=
-1.
5. 1. f(z)=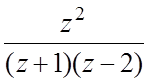 , а)
z0= -1, б) 3< | z-2 | <¥;
, а)
z0= -1, б) 3< | z-2 | <¥;
f(z)=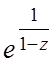 , z0=0;
, z0=0;
f(z)= 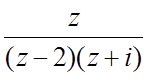 , z0=¥;
, z0=¥;
f(z)= 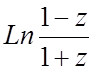 , z0=¥.
, z0=¥.
2. f(z)=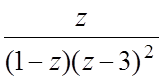 , а)
z0= 0, б) 2< | z-3 | <¥;
, а)
z0= 0, б) 2< | z-3 | <¥;
f(z)=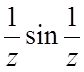 , z0=0;
, z0=0;
f(z)= 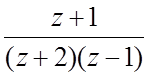 , z0=¥;
, z0=¥;
f(z)=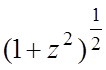 , z0=¥.
, z0=¥.
3. f(z)=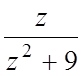 , а)
z0= 3i, б) 3< | z |
<¥;
, а)
z0= 3i, б) 3< | z |
<¥;
f(z)=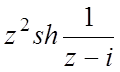 , z0=i;
, z0=i;
f(z)= 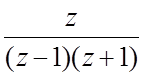 , z0=¥;
, z0=¥;
f(z)=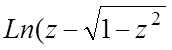 , z0=¥.
, z0=¥.
4. f(z)=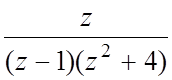 , а)
z0= 1, б)
, а)
z0= 1, б) ![]() < | z-2i
| <4;
< | z-2i
| <4;
f(z)=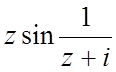 , z0=
-i;
, z0=
-i;
f(z)= 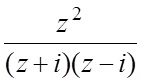 , z0=¥;
, z0=¥;
f(z)=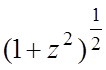 , z0=¥.
, z0=¥.
6. 1. 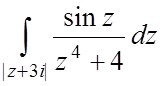 ;
; 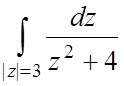 ;
; 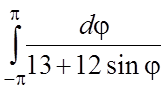 .
.
2. 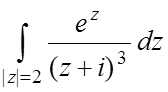 ;
; 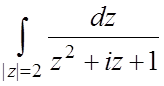 ;
; 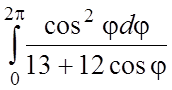 .
.
3. 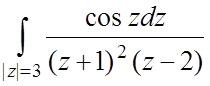 ;
; 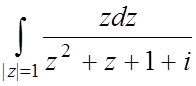 ;
; 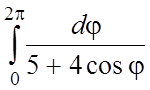 .
.
4. 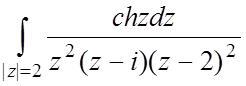 ;
; 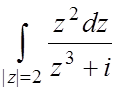 ;
; 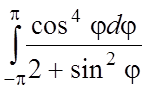 .
.
7. 1. 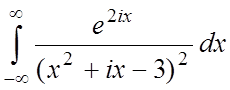 ;
; 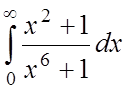 ;
; 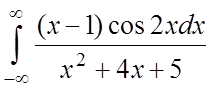 ;
;
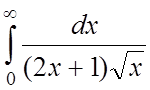 ;
; 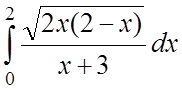 ;
; 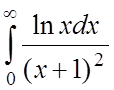 .
.
2. 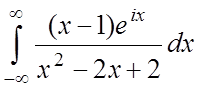 ;
; 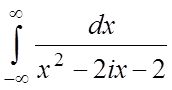 ;
; 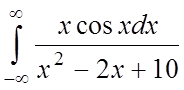 ;
;
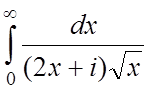 ;
; 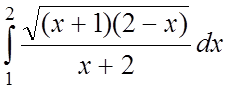 ;
; 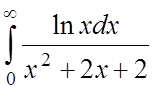 .
.
3. 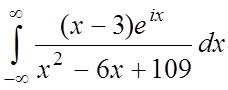 ;
; 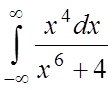 ;
; 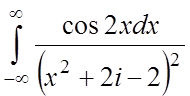 ;
;
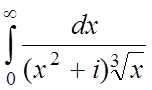 ;
; 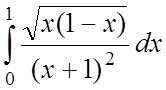 ;
; 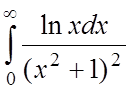 .
.
4. 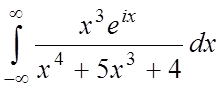 ;
; 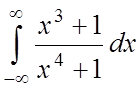 ;
; 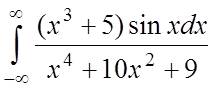 ;
;
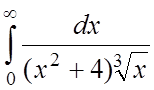 ;
; 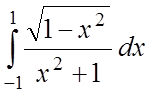 ;
; 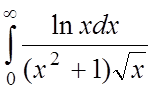 .
.
СПИСОК ЛИТЕРАТУРЫ.
1. Кудрявцев Л.Д, Курс математического анализа. -М.: Высшая школа, 1988.- Т 1,2.
2. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. -М.: Наука, 1988.
3. Сидоров Ю.В. Федорюк Н.В., Шабунин М.И. Лекции по тоерии функций комплексного переменного. - М.: Наука, 1989.
4. Сборник задач по теории аналитических функций /под ред. Евграфова М.А. -М.: Наука, 1972.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.