ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5.
Тема: Функции комплексного переменного. Условия Коши-Римана. Геометрический смысл производной.
Пусть на
множестве ![]() комплексной плоскости
комплексной плоскости ![]() определена комплекснозначная функция
определена комплекснозначная функция ![]() , т.е. каждой точке
, т.е. каждой точке ![]() поставлено
в соответствие комплексное число
поставлено
в соответствие комплексное число ![]() . Эту функцию можно
представить в виде
. Эту функцию можно
представить в виде ![]() , где
, где ![]() ,
, ![]() . Таким образом, задание комплекснозначной
функции комплексного переменного эквивалентно заданию пары действительных
функций от действительных переменных.
. Таким образом, задание комплекснозначной
функции комплексного переменного эквивалентно заданию пары действительных
функций от действительных переменных.
Функция ![]() , определенная в некоторой окрестности
точки
, определенная в некоторой окрестности
точки ![]() , называется дифференцируемой в точке
, называется дифференцируемой в точке ![]() , если существует конечный предел
, если существует конечный предел 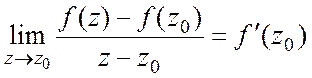 .
.
Так как свойства алгебраических действий и предельного перехода сохраняются при переходе к функциям комплексного переменного, то сохраняются и правила дифференцирования суммы, произведения, частного двух функций, а также правила дифференцирования сложной и обратной функций.
Условие
Коши-Римана: для того, чтобы функция ![]() =
=![]() +
+![]() была дифференцируемой в
точке
была дифференцируемой в
точке ![]() необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
1. функции ![]() ,
, ![]() были
дифференцируемы в точке
были
дифференцируемы в точке ![]() ;
;
2. в точке ![]() выполнялись условия Коши-Римана
выполнялись условия Коши-Римана 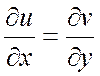 ,
, 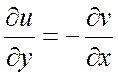 .
.
С учетом этих
условий производную ![]() можно представить в виде:
можно представить в виде: 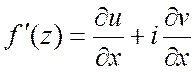 .
.
Условия
Коши-Римана в полярных координатах имеют вид: 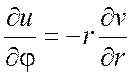 ,
, 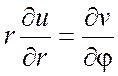 .
.
Пусть ![]() -произвольная точка некоторой гладкой
кривой
-произвольная точка некоторой гладкой
кривой ![]() , лежащей в области определения функции
, лежащей в области определения функции ![]() - области
- области ![]() ,
, ![]() -образ этой кривой,
-образ этой кривой, ![]() .
Через
.
Через ![]() обозначим угол, образованный касательной к
кривой
обозначим угол, образованный касательной к
кривой ![]() в точке
в точке ![]() , через
, через ![]() - угол, образованный касательной к кривой
- угол, образованный касательной к кривой ![]() в точке
в точке ![]() . Угол
. Угол ![]() называется углом поворота кривой
называется углом поворота кривой ![]() в точке
в точке ![]() при
отображении
при
отображении ![]() .
.
Пусть ![]() -произвольная точка кривой
-произвольная точка кривой ![]() , расположенная достаточно близко к точке
, расположенная достаточно близко к точке ![]() ,
, ![]() ,
, ![]() . Предел
. Предел 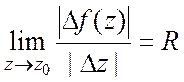 называется
коэффициентом линейного растяжения кривой
называется
коэффициентом линейного растяжения кривой ![]() в точке
в точке
![]() при отображении
при отображении ![]() ,
или просто линейным растяжением.
,
или просто линейным растяжением.
Имеет место
утверждение: если ![]() - дифференцируема в некоторой
окрестности точки
- дифференцируема в некоторой
окрестности точки ![]() и
и ![]() , то
, то ![]()
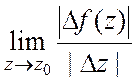 и
и ![]() .
.
Якобиан дифференцируемого в точке ![]() отображения
отображения ![]() =
=![]() +
+![]() равен
равен
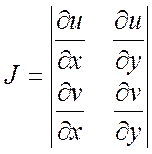 =
= 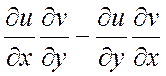 =
=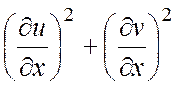 =
= ![]() .
.
Поэтому
1) если
обозначить область определения дифференцируемой на ней функции ![]() через
через ![]() , ее
образ
, ее
образ ![]() :
: ![]() =
=![]() , то площадь области D равна
, то площадь области D равна ![]() =
=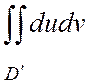 =
= =
=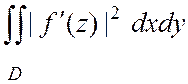 ;
;
2) если ![]() и
и ![]() -ее
образ при отображении
-ее
образ при отображении ![]() :
: ![]() , то
длина кривой
, то
длина кривой ![]() -
- ![]() вычисляется
по формуле
вычисляется
по формуле ![]() =
=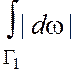 =
=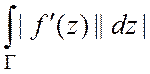 .
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6-8.
Тема: Элементарные функции.
I. Дробно-линейные отображения.
Функция
комплексного переменного 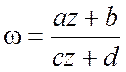 ,
, ![]() , a,b,c,d-комплексные
числа, называется дробно-линейной. При с=0 функция
, a,b,c,d-комплексные
числа, называется дробно-линейной. При с=0 функция ![]() является
линейной
является
линейной 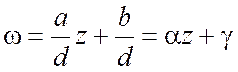 .
.
Перечислим некоторые свойства дробно-линейных отображений:
1. Дробно-линейная функция конформно отображает расширенную
комплексную плоскость ![]() на расширенную комплексную
плоскость
на расширенную комплексную
плоскость ![]() .
.
2. Произведение дробно-линейных отображений, а также функция, обратная к дробно-линейной, являются дробно-линейными функциями.
3. При дробно-линейном отображении пара точек, симметричных относительно окружности, переходит в пару точек, симметричных относительно образа этой окружности.
4. При дробно-линейном отображении образом любой окружности или прямой является окружность или прямая (круговое свойство).
Действительно,
уравнение любой окружности или прямой на комплексной плоскости имеет вид: ![]() =0 (при a=0-
прямая). Так как
=0 (при a=0-
прямая). Так как ![]() ,
, 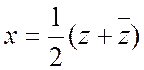 ,
, 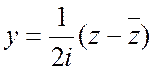 , то уравнение переписывается в виде
, то уравнение переписывается в виде 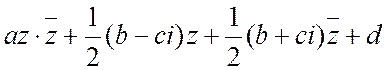 =0 или
=0 или ![]() =0, где
D=b-ic. Дробно-линейную же функцию представим в виде
=0, где
D=b-ic. Дробно-линейную же функцию представим в виде 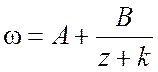 , где
, где 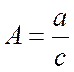 ,
, 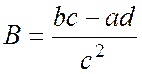 ,
, 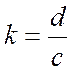 . Тогда
она сводится к последовательному выполнению преобразований
. Тогда
она сводится к последовательному выполнению преобразований ![]() ,
, 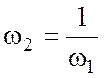 ,
, ![]() , из которых
, из которых ![]() и
и ![]() круговым свойством обладают, так как они
линейные.
круговым свойством обладают, так как они
линейные.
Докажем, что
отображение 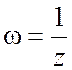 также обладает круговым свойством.
также обладает круговым свойством.
Подставим в
уравнение окружности ![]() =0 вместо
=0 вместо ![]() выражение
выражение
![]() . Получаем:
. Получаем:
![]() =0 - окружность.
=0 - окружность.
Некоторые частные случаи.
1. Если окружность проходит через начало координат ![]() =0), то ее образом является прямая общего
положения.
=0), то ее образом является прямая общего
положения.
2. Если прямая проходит через начало координат (![]() =0), то ее образом является прямая,
проходящая через начало координат.
=0), то ее образом является прямая,
проходящая через начало координат.
3. Образом окружности общего положения является окружность общего положения.
4. Образом прямой общего положения является окружность, проходящая через начало координат.
II. Функция
Жуковского 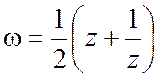 .
.
Она регулярна в точках z¹0, ¥, однолистна в каждой из областей: 1) |z|>1; 2) |z|<1; 3) Imz>0; 4) Imz<0. Образами первых двух областей при конформном отображении функцией Жуковского является плоскость w с разрезом по отрезку [-1,1], двух последних- плоскость w с разрезами по лучам (-¥,-1] и [1, + ¥).
III. Функция w=![]() .
.
Функция w=![]() определяется формулой
определяется формулой ![]() =ex(cosy+isiny),
z=x+iy. Она регулярна во всей плоскости z,
однолистна в любой области, не содержащей двух различных точек z1, z2,
связанных равенством: z1 -z2=2kpi, k=±1, ±2,....
В частности, функция
=ex(cosy+isiny),
z=x+iy. Она регулярна во всей плоскости z,
однолистна в любой области, не содержащей двух различных точек z1, z2,
связанных равенством: z1 -z2=2kpi, k=±1, ±2,....
В частности, функция ![]() однолистна в полосах 2kp<Imz<(2k+2) p, k=±1, ±2,.... Она конформно отображает эти области
однолистности на плоскость w с разрезом
по лучу [0,+¥).
однолистна в полосах 2kp<Imz<(2k+2) p, k=±1, ±2,.... Она конформно отображает эти области
однолистности на плоскость w с разрезом
по лучу [0,+¥).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.