Функции комплексного переменного. Условия Коши-Римана. Геометрический смысл производной. Элементарные функции. Интегрирование функций комплексного переменного. Теоремы Коши. Ряд Тейлора (Практические занятия № 5-10), страница 2

IV. Функция w=lnz.

Эта функция, обратная к функции w= является аналитической в плоскости z с выколотыми точками z=0, ¥. В плоскости z с разрезом, соединяющим эти точки, распадается на бесконечное число регулярных ветвей.

V. Функция .

Эта функция регулярна во всех точках плоскости z, однолистна в любой области, в которой нет различных точек z₁ и z₂, симметричных относительно точки (0,0). В частности,  однолистна в любом секторе 2kp<argz<b+2kp, b£, k=±1, ±2,.... Она конформно отображает эти области на плоскость w, в области вида 2kp<argw<bn+2kp, k=±1, ±2,....

VI. Функция w=.

Эта функция обратна к функции , аналическая во всей плоскости z, исключая точки z=0, z=¥. В плоскости z с разрезом, соединяющим эти точки, распадается на n регулярных ветвей.

VII. Функция

Функция  определяется формулой =, >0. Областью однолистности является, например, сектор 0<<b, b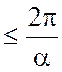, который функция конформно отображает на сектор 0<arg<.

VIII. Тригонометрические и гиперболические функции.

Эти функции выражаются через показательную функцию по формулам:

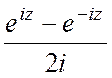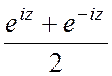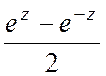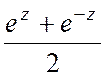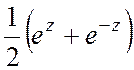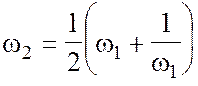sinz=, cosz=, shz=, chz=. Эти функции регулярны в своих областях однолистности, конформно отображают их на плоскость . Чтобы найти образ области однолистности каждой такой функции, прибегают к такому приему: расписывают функцию как суперпозицию рассмотренных выше функций. Например, =chz= является суперпозицией двух функций: w₁= и . В результате последовательного выполнения отображений w₁ и w₂ получаем образ отображения chz. Область же однолистности находится по такой схеме: предполагаем, что две различные точки z₁ и z₂ плоскости z переходят при отображении в одну точку плоскости w. В результате получаем условия, которым не должны удовлетворять точки области однолистности. Для функции =chz имеем: z₁¹z₂, но ch z₁=chz₂ = =0  z₁-z₂=2kpi x₁=x₂ и 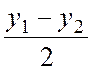= kp, k=0, ±1, ±2,.... Последним соотношениям удовлетворяет, например, область 0<Imz<p, Rez>0.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9, 10.

Тема: Интегрирование функций комплексного переменного.

 Теоремы Коши. Ряд Тейлора.

I. Пусть f- комплекснозначная непрерывная ограниченная функция, определенная в точке z.

1. Если  ограниченное замкнутое измеримое множество на плоскости, то интеграл от функции  по области  определяется равенством

.

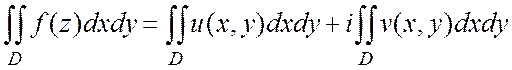2. Интеграл от функции f по гладкой кривой G определяется следующим образом: 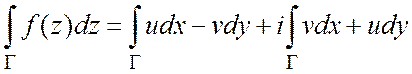. Существование интеграла в левой части равенства  равносильно существованию криволинейных интегралов от действительных функций в правой части равенства. Если параметрическим уравнением кривой G является функция z(t), tÎ[a,b], то =.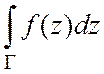

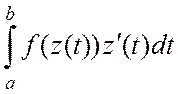II. Ниже приводятся формулировки теоремы Коши для различных областей.

1. Пусть функция  дифференцируема в односвязной области . Тогда интеграл от  по любой замкнутой кривой , лежащей в области , равен нулю: 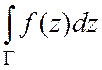=0.

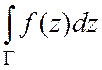2. Пусть - ограниченная односвязная область с кусочно-гладкой границей , функция  дифференцируема в области  и непрерывна вплоть до ее границы. Тогда =0.

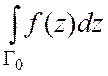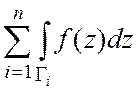3. Пусть граница  многосвязной области  состоит из замкнутой кусочно-гладкой кривой  и попарно непересекающихся замкнутых кусочно-гладких кривых , расположенных внутри , функция  дифференцируема в области  и непрерывна вплоть до ее границы. Тогда +=0.

Теорема 1. Пусть  дифференцируема в односвязной области . Тогда она имеет в этой области первообразную .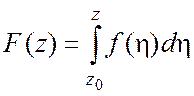

Следствие Пусть  непрерывна в области  и интеграл от этой функции по любой замкнутой кривой, лежащей в области , равен нулю. Тогда функция 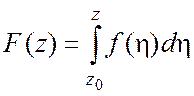 есть первообразная функции .

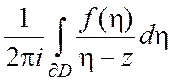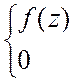
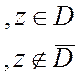Теорема 2. (интегральная формула Коши). Пусть функция ) дифференцируема в ограниченной области  и непрерывна вплоть до ее границы, состоящей из конечного числа замкнутых кусочно-гладких кривых. Тогда                                     =  и  

=

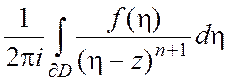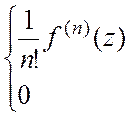
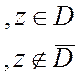
III. Известно, что каждая регулярная каком-либо круге  функция  разлагается в этом круге в сходящийся степенной ряд

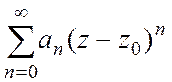=, где 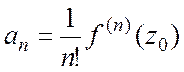, который называется рядом Тейлора функции  в окрестности точки .

Некоторые приемы разложения в степенной ряд.

1. Если - рациональная функция, то ее полезно разложить на сумму более простых дробей (стремиться к полному разложению на простейшие дроби не обязательно).

В некоторых случаях рациональную функцию можно упростить умножением числителя и знаменателя на подходящий множитель.

2. Если  представляет собой комбинацию из показательных и тригонометрических функций, бывает полезно преобразовать функцию к комбинации только показательных функций.

3. Если функция  представляет собой отношение двух функций, ряды Тейлора для которых известны, бывает полезным воспользоваться методом неопределенных коэффициентов.

4. Использование известных разложений функций в ряд Тейлора.