Литература
Лаврентьев, Шабат: «Методы теории функций комплексного переменного»;
Сидоров, Федорюк, Шабунин: «Лекции по теории функций комплексного переменного»;
Бекарева: «Теория функций комплексного переменного» (учебное пособие)
Определение. Комплексным числом ![]() будем называть пару
будем называть пару ![]() , если для таких пар определено
отношение равенства и операций сложения и умножения следующим образом:
, если для таких пар определено
отношение равенства и операций сложения и умножения следующим образом:
1)
(1) ![]() ;
;
2)
(2) ![]() ;
;
3)
(3) ![]() .
.
Все множество комплексных чисел будем обозначать через ![]() .
.
Рассмотрим комплексные числа вида ![]() . Тогда
. Тогда ![]() ,
, ![]() .
Т.е. числа того вида есть вещественные и
.
Т.е. числа того вида есть вещественные и ![]() . Тогда получили, что
. Тогда получили, что ![]() .
.
Рассмотрим комплексные числа вида 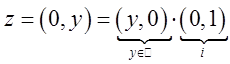 . Такие числа будем называть мнимыми
и обозначать, как
. Такие числа будем называть мнимыми
и обозначать, как ![]() .
.
Замечание. В некоторой литературе (чаще всего в
электротехнике) вместо ![]() используют
используют
![]() (йот).
(йот).
![]() (4). Тогда
(4). Тогда
![]() и называется мнимой
единицей.
и называется мнимой
единицей.
Исторически комплексные числа были введены из тех соображений, чтобы любые алгебраические уравнения (в первую очередь с четными степенями) имели корни.
В частности справедлива общая теорема алгебры.
Теорема. В комплексных числах любое алгебраическое
уравнение ![]() -ого порядка
имеет ровно
-ого порядка
имеет ровно ![]() корней с учетом
их кратности:
корней с учетом
их кратности: ![]() , где
, где ![]() - корень кратности
- корень кратности ![]() .
.
Возьмем любое комплексное число ![]() . С помощью (2) получим
. С помощью (2) получим ![]() - алгебраическая форма записи.
В алгебраической форме записи сложение комплексных чисел выполняется, как
обычное алгебраическое сложение с приведением подобных членов по
- алгебраическая форма записи.
В алгебраической форме записи сложение комплексных чисел выполняется, как
обычное алгебраическое сложение с приведением подобных членов по ![]() :
: 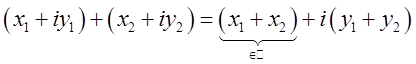 . А
умножение комплексных чисел, как обычное алгебраическое умножение двучленов с
учетом (4).
. А
умножение комплексных чисел, как обычное алгебраическое умножение двучленов с
учетом (4).
Определение. В алгебраической форме записи число ![]() называется вещественной или действительной
частью комплексного числа
называется вещественной или действительной
частью комплексного числа ![]() и
обозначается
и
обозначается ![]() , а
, а ![]() - мнимой частью комплексного
числа и обозначается
- мнимой частью комплексного
числа и обозначается ![]() .
Тогда
.
Тогда ![]() (5).
(5).
Замечание. ![]() ,
т.е. мнимая единица не входит в мнимую часть комплексного числа.
,
т.е. мнимая единица не входит в мнимую часть комплексного числа.
Пример. ![]() .
.
Определение.Если комплексное число ![]() , то комплексное число
, то комплексное число ![]() называется сопряженным числу
называется сопряженным числу
![]() .
.
Дополнение к основной теореме алгебры: Если алгебраическое уравнение имеет в качестве своих коэффициентов только вещественные числа, то число его комплексных корней (если они есть) будет обязательно четным, и эти комплексные корни будут распадаться на сопряженные пары.
Теорема. 1) для того, чтобы комплексное число
совпадало с сопряженным себе необходимо и достаточно, чтобы оно было вещественным:
![]() ; 2) для того, чтобы
комплексное число при сопряжении меняло знак необходимо и достаточно, чтобы оно
было мнимым:
; 2) для того, чтобы
комплексное число при сопряжении меняло знак необходимо и достаточно, чтобы оно
было мнимым: ![]() .
.
Обратные операции над комплексными числами (операции вычитания и деления)
Покажем, что для любых комплексных чисел ![]() и
и ![]() существует единственное комплексное
число
существует единственное комплексное
число ![]() такое, что
такое, что ![]() , и будет называть это число разностью
чисел
, и будет называть это число разностью
чисел ![]() и
и ![]() :
: ![]() .
.
Доказательство. Предположим, что ![]() . Тогда
. Тогда 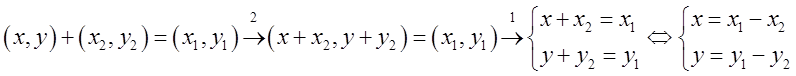 .
.
Таким образом ![]() (6).
(6).
Аналогично покажем, что для любых комплексных чисел ![]() и
и ![]() существует единственное комплексное
число
существует единственное комплексное
число ![]() такое, что
такое, что ![]() , которое будем называть отношением
, которое будем называть отношением
![]() к
к ![]() :
: 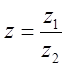 .
.
Доказательство.
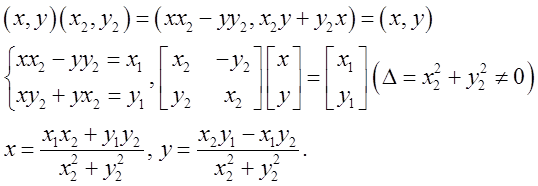
Тогда 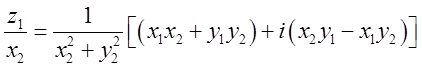 . Рассмотрим
. Рассмотрим
![]() . Таким образом
. Таким образом 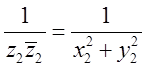 , тогда получаем, что
, тогда получаем, что 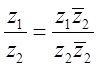 .
.
Рассмотрим умножение комплексного числа на вещественное: ![]() . Умножение вещественного числа на
комплексное выполняется покомпонентно.
. Умножение вещественного числа на
комплексное выполняется покомпонентно.
Операции сложения и умножения комплексных чисел обладают свойствами коммутативности, ассоциативности и дистрибутивности.
Домашнее задание. Доказать.
Замечание. Как нетрудно увидеть по отношению к операциям сложения, вычитания и умножения на вещественное число, комплексные числа ведут себя точно также как двумерные векторы.
Алгебраическая форма записи соответствует декартовым координатам.
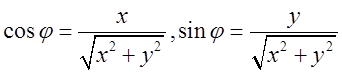 (8). Тогда
(8). Тогда
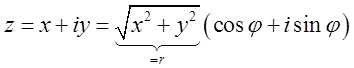 .
.
Определение. Величина ![]() называется модулем комплексного
числа
называется модулем комплексного
числа ![]() , а угол
, а угол ![]() , удовлетворяющий соотношениям (8)
называется аргументом комплексного числа
, удовлетворяющий соотношениям (8)
называется аргументом комплексного числа ![]() :
: ![]() .
.
Замечание. Существует счетное множество углов ![]() , удовлетворяющих соотношениям (8),
которые отличаются друг от друга на
, удовлетворяющих соотношениям (8),
которые отличаются друг от друга на ![]() :
:
![]() .
.
Чтобы не возникало двусмысленности, будем называть главным
значением аргумента угол, который будет лежать в промежутке ![]() :
: ![]() , тогда
, тогда
![]() .
.
Если некоторое действие над комплексными числами требует
использования понятия аргумента, то по умолчанию всегда предполагается, что все
участвующие в формуле аргументы – это либо главные значения, либо им
соответствует одно и то же число ![]() .
.
В свете введенных понятий модуля и аргумента, запишем еще
одну формулу ![]() (9) – тригонометрическая
форма записи комплексного числа, которой соответствуют полярные координаты.
(9) – тригонометрическая
форма записи комплексного числа, которой соответствуют полярные координаты.
![]() . Тогда
. Тогда
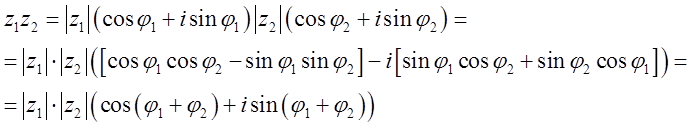
Тогда ![]() (10).
(10).
Домашнее задание. Доказать, что ![]() .
.
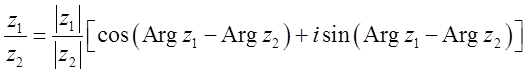 (11).
(11).
При умножении комплексных чисел их модули умножаются, а аргументы складываются, а при делении модули делятся, а аргументы вычитаются.
Поскольку аргументы комплексных чисел при их умножении и
делении ведут себя такие, как показатели степеней или логарифмов, Эйлер ввел
формулу: ![]() (12), для
которой это свойство остается справедливым и которое расширяет понятие обычной
вещественной экспоненты.
(12), для
которой это свойство остается справедливым и которое расширяет понятие обычной
вещественной экспоненты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.