Задача 12. Вычислить несобственный интеграл с помощью вычетов.
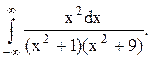
Решение. В данном случае в верхней полуплоскости расположены два полюса z=i и z=3i
функции 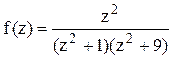 .
.
Тогда 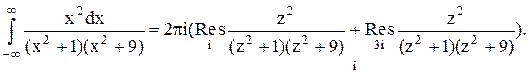
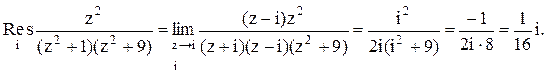
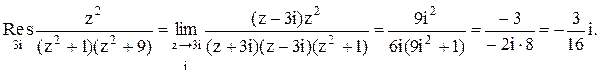 Следовательно.
Следовательно. 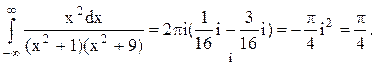
Ответ. 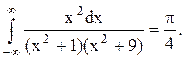
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
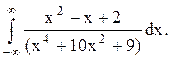
Решение. В данном случае в верхней полуплоскости расположены два полюса z=i и z=3i.
Функции 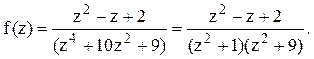
Тогда 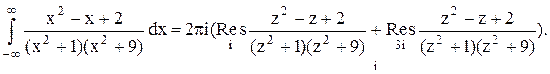
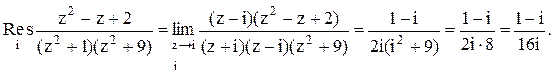
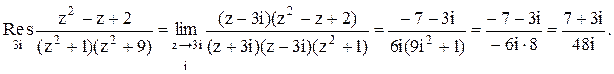
Следовательно. 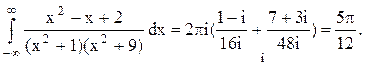
Ответ. 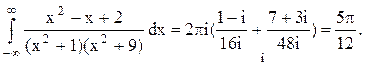
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
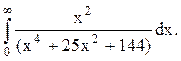
Решение. Найдём корни знаменателя функции 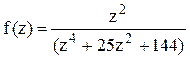 , решая биквадратное уравнение: (z2)2+25(z2)+144=0,
, решая биквадратное уравнение: (z2)2+25(z2)+144=0,
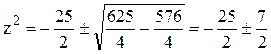 . Следовательно,
. Следовательно, ![]() . В данном случае в верхней
полуплоскости расположены два полюса z=3i и z=4i
функции
. В данном случае в верхней
полуплоскости расположены два полюса z=3i и z=4i
функции 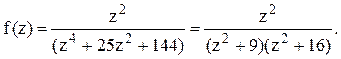
Тогда 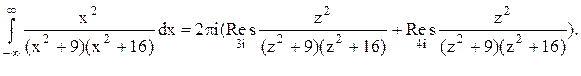
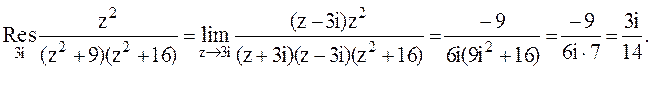
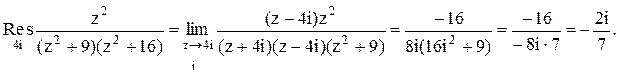
Следовательно. 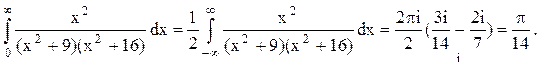
Ответ. 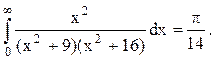
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
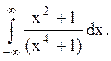
Решение. Найдём корни знаменателя функции 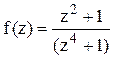 :
: 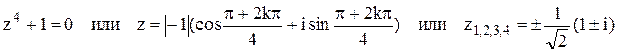 .
Следовательно, два корня из четырёх находятся в верхней полуплоскости:
.
Следовательно, два корня из четырёх находятся в верхней полуплоскости: 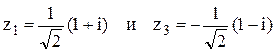 .
.
Тогда 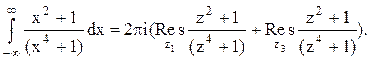
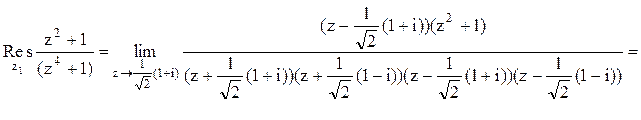
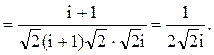
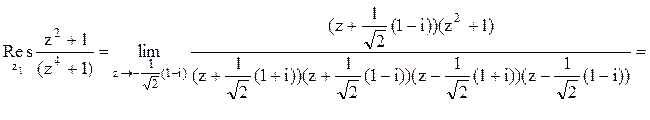
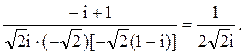
Следовательно. 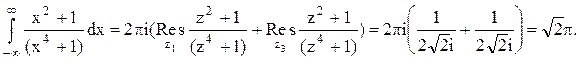
Ответ. 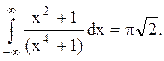
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
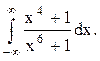
Решение. Рассмотрим функцию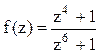 .
Найдём полюсы этой функции:
.
Найдём полюсы этой функции: ![]() . В данном случае в
верхней полуплоскости расположены три полюса из шести:
. В данном случае в
верхней полуплоскости расположены три полюса из шести: ![]()
Тогда 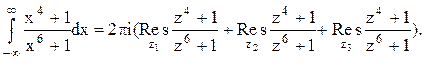
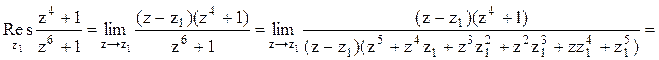
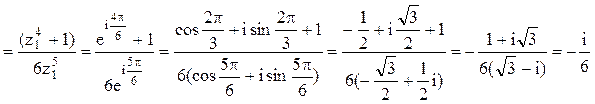 .
.
При разложении ![]() на множители было
учтено, что
на множители было
учтено, что ![]() . Аналогично,
. Аналогично,
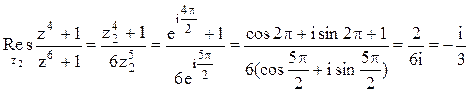 .
.
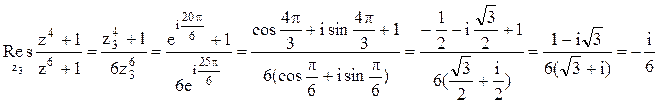
Следовательно. 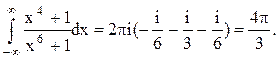
Ответ. 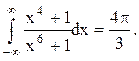
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
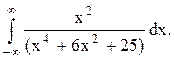
Решение. Найдём корни знаменателя функции 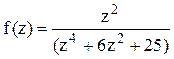 , решая биквадратное уравнение: (z2)2+6(z2)+25=0,
, решая биквадратное уравнение: (z2)2+6(z2)+25=0,
![]() . Число
. Число ![]() геометрически расположено во второй
четверти комплексной плоскости. Следовательно, один из корней
геометрически расположено во второй
четверти комплексной плоскости. Следовательно, один из корней ![]() обязательно будет расположен в первой
четверти. Найдём этот корень. Если
обязательно будет расположен в первой
четверти. Найдём этот корень. Если 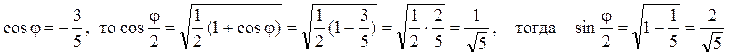 Итак,
Итак, 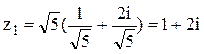 . Тогда
. Тогда 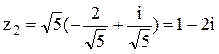 .Аналогично,
число
.Аналогично,
число ![]() геометрически
расположено в третьей четверти комплексной плоскости. Следовательно, один из
корней
геометрически
расположено в третьей четверти комплексной плоскости. Следовательно, один из
корней ![]() обязательно будет расположен во второй
четверти. Это значит, что
обязательно будет расположен во второй
четверти. Это значит, что 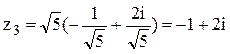 . Тогда
. Тогда 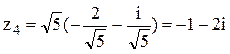 .В данном случае в верхней полуплоскости
расположены два простых полюса z1 и z3 функции
.В данном случае в верхней полуплоскости
расположены два простых полюса z1 и z3 функции 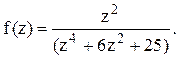
Тогда 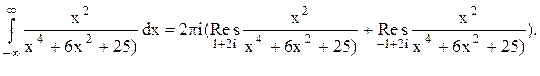
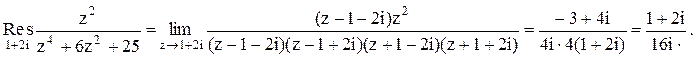
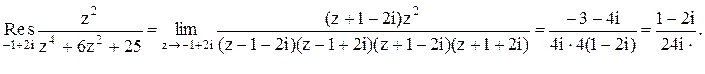
Следовательно. 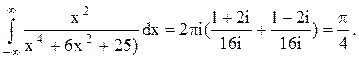
Ответ. 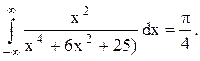
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
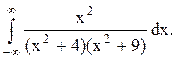
Решение. Найдём корни знаменателя функции 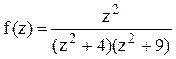 . Приравнивая знаменатель к нулю, получим:
. Приравнивая знаменатель к нулю, получим: ![]() . В данном случае в верхней полуплоскости
расположены два полюса z=2i и z=3i функции
. В данном случае в верхней полуплоскости
расположены два полюса z=2i и z=3i функции 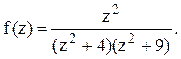
Тогда 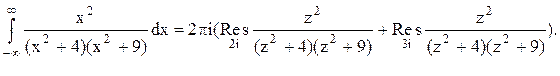
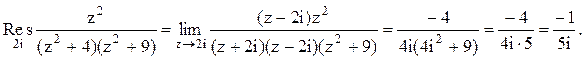
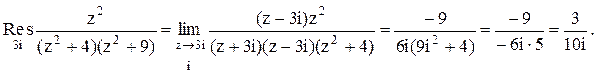
Следовательно. 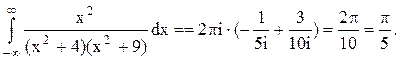
Ответ. 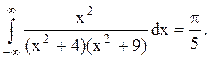
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
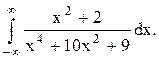
Решение. Найдём корни знаменателя функции 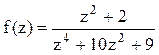 , решая биквадратное уравнение: (z2)2+10(z2)+9=0,
, решая биквадратное уравнение: (z2)2+10(z2)+9=0,
![]() . Следовательно,
. Следовательно, ![]() .
.
В верхней полуплоскости находятся два корня: z1=i z2=3i Тогда 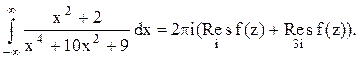
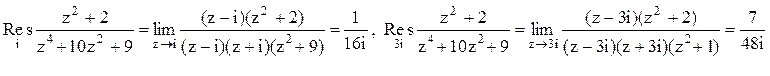 .
.
Следовательно. 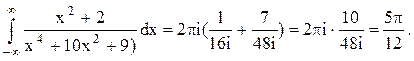
Ответ. 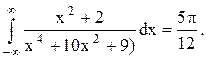
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
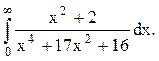
Решение. Найдём корни знаменателя функции 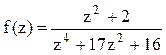 , решая биквадратное уравнение: (z2)2+17(z2)+16=0,
, решая биквадратное уравнение: (z2)2+17(z2)+16=0,
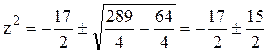 . Следовательно,
. Следовательно, ![]() .
.
В верхней полуплоскости находятся два корня: z1=i z2=4i Тогда 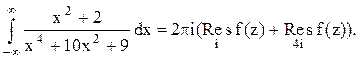
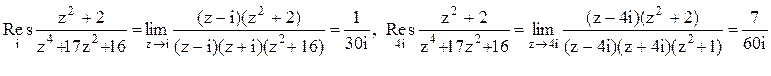 .
.
Следовательно. 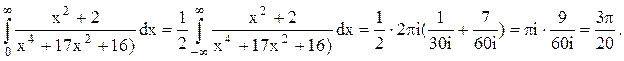
Ответ. 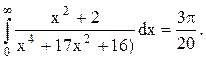
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
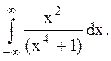
Решение. Найдём корни знаменателя функции 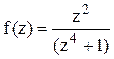 :
: 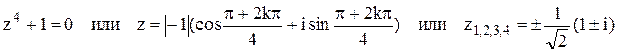 .
Следовательно, два корня из четырёх находятся в верхней полуплоскости:
.
Следовательно, два корня из четырёх находятся в верхней полуплоскости: 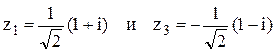 .
.
Тогда 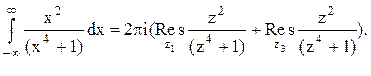
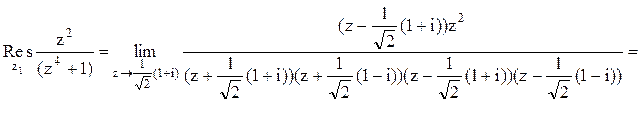
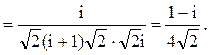
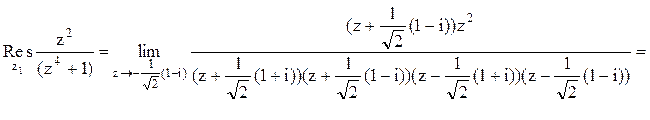
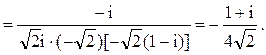
Следовательно. 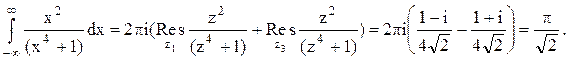
Ответ. 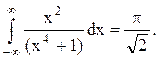
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
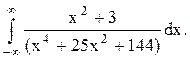
Решение. Найдём корни знаменателя функции 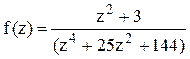 , решая биквадратное уравнение: (z2)2+25(z2)+144=0,
, решая биквадратное уравнение: (z2)2+25(z2)+144=0,
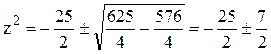 . Следовательно,
. Следовательно, ![]() . В данном случае в верхней
полуплоскости расположены два полюса z=3i и z=4i
функции
. В данном случае в верхней
полуплоскости расположены два полюса z=3i и z=4i
функции 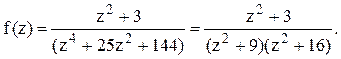
Тогда 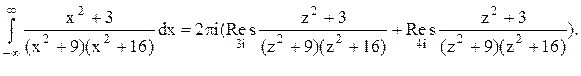
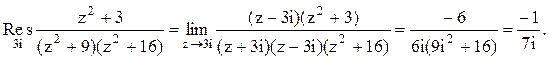
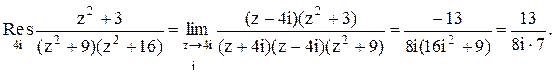
Следовательно. 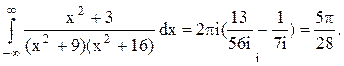
Ответ. 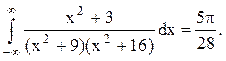
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
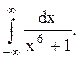
Решение. Найдём корни знаменателя функции 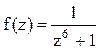 :
: ![]() .
Полагая здесь k=0, 1, 2, находим три корня, лежащие в верхней половине
комплекснойплоскости:
.
Полагая здесь k=0, 1, 2, находим три корня, лежащие в верхней половине
комплекснойплоскости: 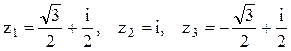 . Остальные три корня
являются сопряжёнными по отношению к найденным корням и находятся в нижней полуплоскости.
Таким образом,
. Остальные три корня
являются сопряжёнными по отношению к найденным корням и находятся в нижней полуплоскости.
Таким образом,
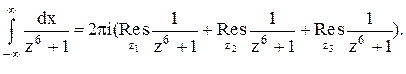
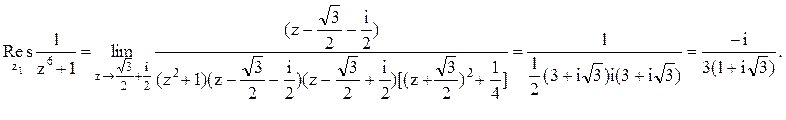

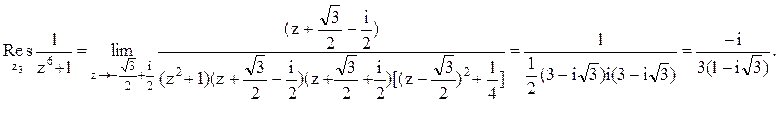
Следовательно. 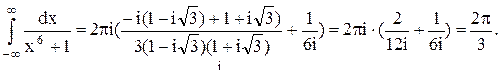
Ответ. 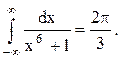
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
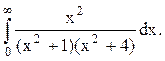
Решение. Корнями знаменателя функции 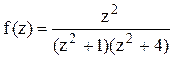 являются числа
являются числа ![]() . В данном случае в верхней
полуплоскости расположены два полюса z=i и z=2i
данной функции.
. В данном случае в верхней
полуплоскости расположены два полюса z=i и z=2i
данной функции.
Тогда 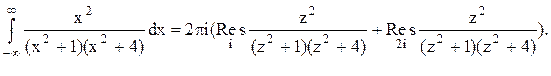
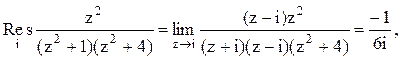
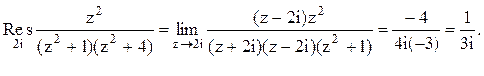
Следовательно. 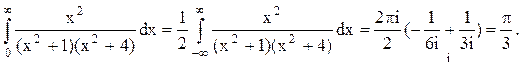
Ответ. 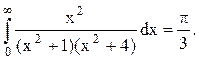
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
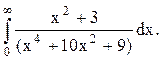
Решение. Найдём корни знаменателя функции 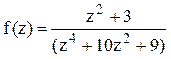 , решая биквадратное уравнение: (z2)2+10(z2)+9=0,
, решая биквадратное уравнение: (z2)2+10(z2)+9=0,
![]() . Следовательно,
. Следовательно, ![]() . В данном случае в верхней
полуплоскости расположены два полюса z=i и z=3i
функции
. В данном случае в верхней
полуплоскости расположены два полюса z=i и z=3i
функции 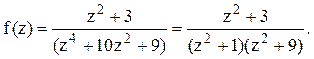
Тогда 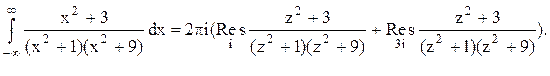
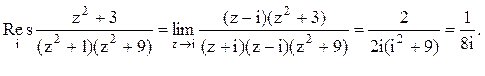
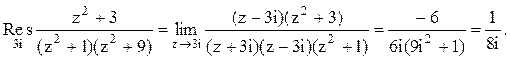
Следовательно. 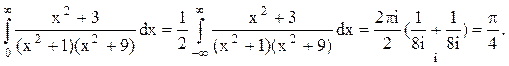
Ответ. 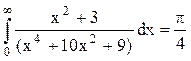 .
.
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
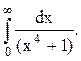
Решение. Найдём корни знаменателя функции 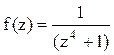 :
: 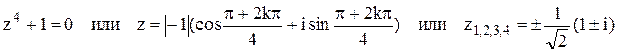 .
Следовательно, два корня из четырёх находятся в верхней полуплоскости:
.
Следовательно, два корня из четырёх находятся в верхней полуплоскости: 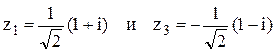 . Тогда
. Тогда 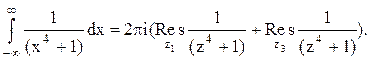
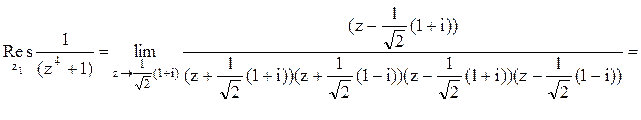
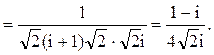
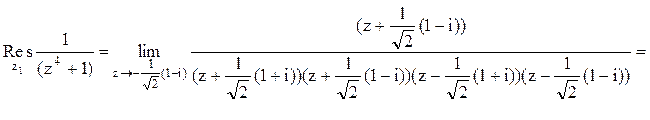
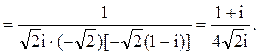 Следовательно.
Следовательно. 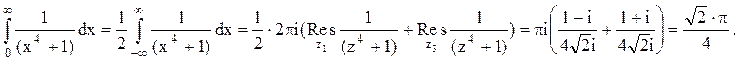
Ответ. 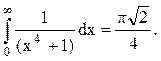
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
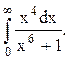
Решение. Найдём корни знаменателя функции 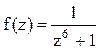 :
: ![]() .
Полагая здесь k=0, 1, 2, находим три корня, лежащие в верхней половине
комплекснойплоскости:
.
Полагая здесь k=0, 1, 2, находим три корня, лежащие в верхней половине
комплекснойплоскости: 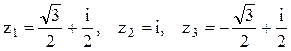 . Остальные три корня
являются сопряжёнными по отношению к найденным корням и находятся в нижней
полуплоскости. Таким образом,
. Остальные три корня
являются сопряжёнными по отношению к найденным корням и находятся в нижней
полуплоскости. Таким образом,
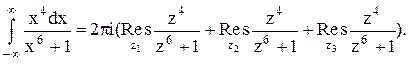
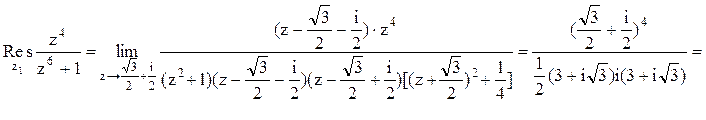
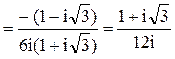 .
. 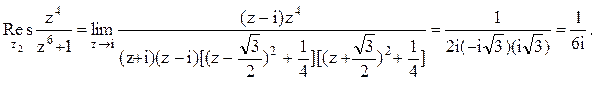
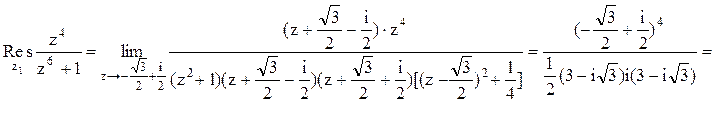
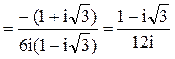 .
.
Следовательно. 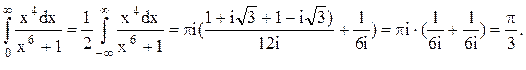
Ответ. 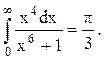
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
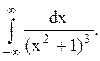
Решение. Корнями знаменателя функции 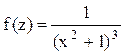 являются числа
являются числа ![]() . В данном случае в верхней
полуплоскости расположен один полюс z=i
данной функции кратности 3. Тогда
. В данном случае в верхней
полуплоскости расположен один полюс z=i
данной функции кратности 3. Тогда 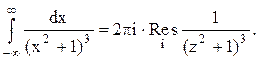
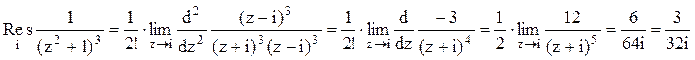
Следовательно. 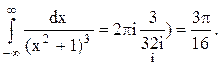
Ответ. 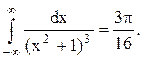
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
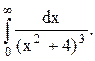
Решение. Корнями знаменателя функции 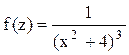 являются числа
являются числа ![]() . В данном случае в верхней
полуплоскости расположен один полюс z=2i данной функции кратности 3. Тогда
. В данном случае в верхней
полуплоскости расположен один полюс z=2i данной функции кратности 3. Тогда 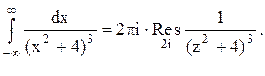
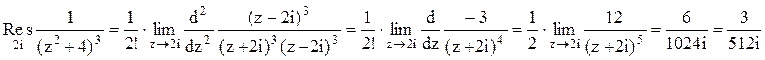 . Следовательно.
. Следовательно. 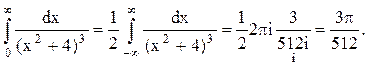
Ответ. 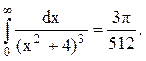
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
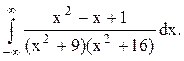
Решение. Корнями знаменателя функции 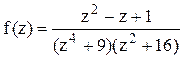 являются числа
являются числа ![]() . В верхней полуплоскости
расположены два полюса z=3i и z=4i данной функции.
. В верхней полуплоскости
расположены два полюса z=3i и z=4i данной функции.
Тогда 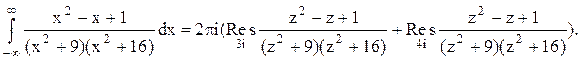
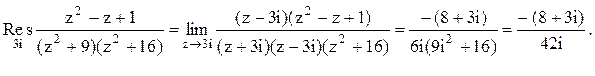
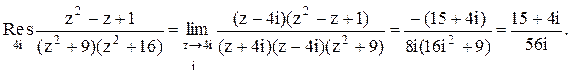
Следовательно. 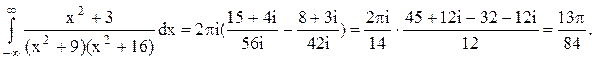
Ответ. 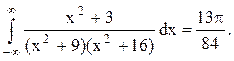
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
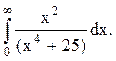
Решение. Найдём корни знаменателя функции 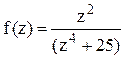 :
: 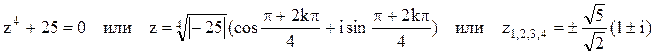 .
Следовательно, два корня из четырёх находятся в верхней полуплоскости:
.
Следовательно, два корня из четырёх находятся в верхней полуплоскости: 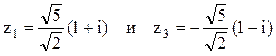 .
.
Тогда 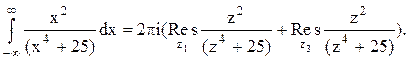
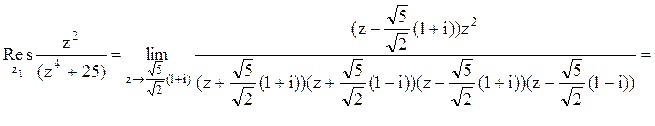
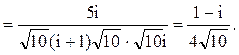
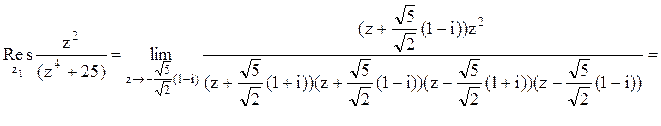
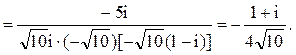 Следовательно.
Следовательно. 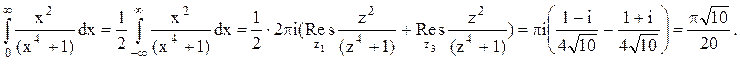
Ответ. 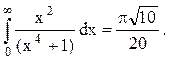
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
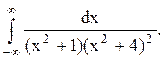
Решение. Корнями знаменателя функции 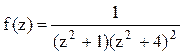 являются числа
являются числа ![]() . В данном случае в верхней
полуплоскости расположены два полюса z=i и z=2i
данной функции.
. В данном случае в верхней
полуплоскости расположены два полюса z=i и z=2i
данной функции.
Тогда 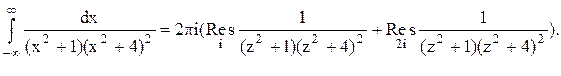
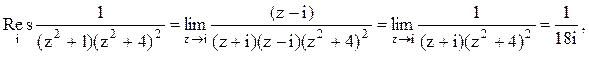
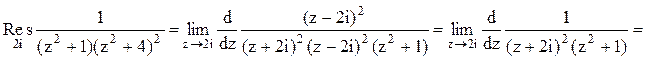
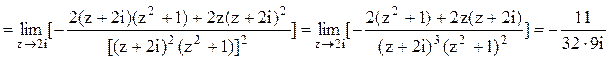 .
.
Следовательно. 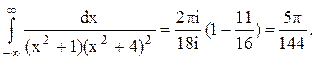
Ответ. 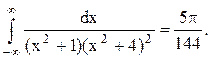
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
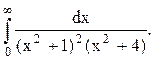
Решение. Корнями знаменателя функции 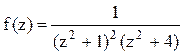 являются числа
являются числа ![]() . В данном случае в верхней
полуплоскости расположены два полюса z=i и z=2i
данной функции.
. В данном случае в верхней
полуплоскости расположены два полюса z=i и z=2i
данной функции.
Тогда 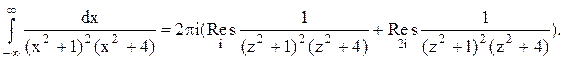
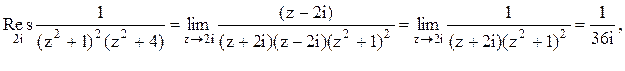
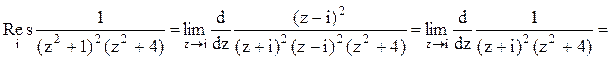
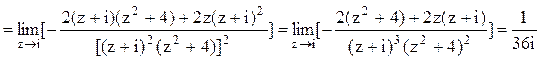 .
.
Следовательно. 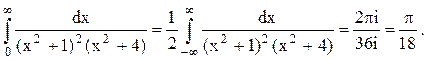
Ответ. 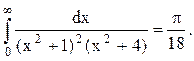
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
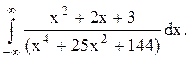
Решение. Найдём корни знаменателя функции 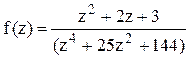 , решая биквадратное уравнение: (z2)2+25(z2)+144=0,
, решая биквадратное уравнение: (z2)2+25(z2)+144=0,
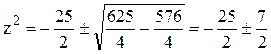 . Следовательно,
. Следовательно, ![]() . В данном случае в верхней
полуплоскости расположены два полюса z=3i и z=4i
функции
. В данном случае в верхней
полуплоскости расположены два полюса z=3i и z=4i
функции 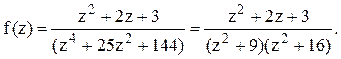
Тогда 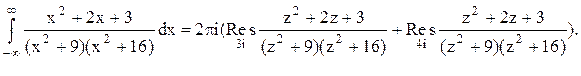
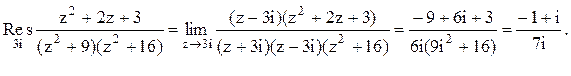
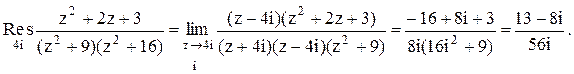
Следовательно. 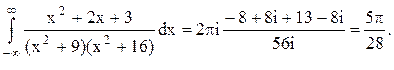
Ответ. 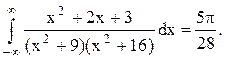
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
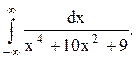
Решение. Знаменатель разлагается на множители ![]() . Корнями знаменателя функции
. Корнями знаменателя функции 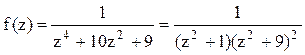 являются числа
являются числа ![]() . В данном случае в верхней
полуплоскости расположены два полюса z=i и z=3i
данной функции.
. В данном случае в верхней
полуплоскости расположены два полюса z=i и z=3i
данной функции.
Тогда 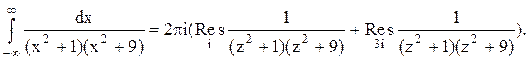
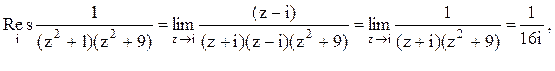
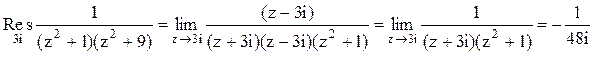 .
.
Следовательно. 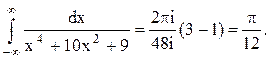
Ответ. 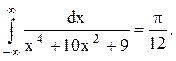
Задача 12. Вычислить несобственный интеграл с помощью вычетов.
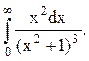
Решение. Корнями знаменателя функции  являются числа
являются числа ![]() . В данном случае в верхней
полуплоскости расположен один полюс z=i
данной функции кратности 3.
. В данном случае в верхней
полуплоскости расположен один полюс z=i
данной функции кратности 3.
Тогда 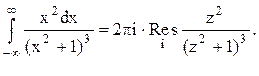
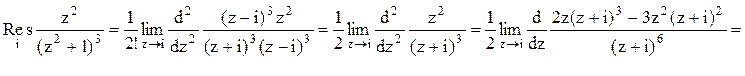
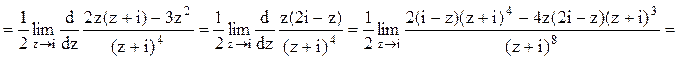
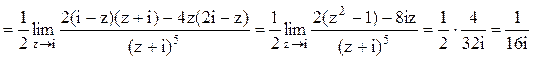
Следовательно. 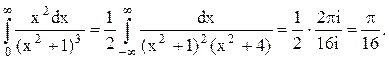
Ответ. 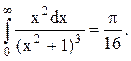
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.