Алгоритмизированные задания по курсу ТОЭ. Анализ переходных процессов: Методическое руководство, страница 8

.

Как следует из схемы (рис.5), в установившемся докоммутационном режиме

.

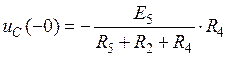Следовательно,

.

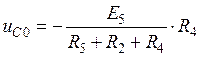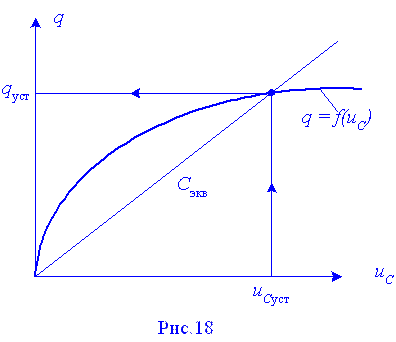
Заданная кулон-вольтная характеристика нелинейного конденсатора q = f(u_C) позволяет определить по значению u_C0 заряд конденсатора q₀ в начальный момент переходного процесса.

Подставив значения q₀и u_C0  в соотношение (30) можно определить заряд конденсатора q₁ в конце первого временного интервала, т.е. в момент  времени t = Dt. Кулон-вольтная характеристика нелинейного конденсатора q = f(u_C)  позволяет по найденному значению q₁ определить соответствующее напряжение на конденсаторе u_C1 в этот же момент времени t = Dt.

        Для k = 1 уравнение (30) принимает вид

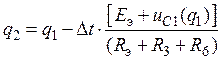,                                              (31)

где q₁ и u_C1 вышенайденные заряд и напряжение на конденсаторе в начале второго временного интервала Dt,  т.е. при t = Dt, а q₂ значение напряжения на конденсаторе в конце второго временного интервала Dt,  т.е. при t = 2Dt. Определив по уравнению (31) q₂  по кулон-вольтной характеристике находится соответствующее напряжение на конденсаторе u_C2 .

 Далее, процесс расчета  уравнения (30) многократно повторяется. При этом определяются q₃  и в момент времени t = 3Dt, .q₄  и в момент времени t = 4Dt  и т.д. Расчет ведется до тех пор, пока рассчитанные значения искомой величины в начале и в конце очередного интервала не совпадут с требуемой точностью. Значения переходного тока в любой рассматриваемый момент времени t = kDt может быть найдено по значению напряжения на конденсаторе из уравнения (27), представленного в соответствующей форме

.

Результаты расчета целесообразно свести в таблицу 4

Таблица 4

Примечание. Для выбора величины временного интервала Dt при численном расчете переходного процесса в нелинейной цепи целесообразно заменить реальный нелинейный элемент условно линейным с параметром, соответствующим установившемуся послекоммутационному режиму цепи (см.рис.18).

Применительно к рассматриваему случаю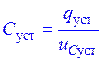

,                       (32)

Для цепи (рис.17) при

.

На заданной кулон-вольтной характеристике

q = f(u_C) нелинейного конденсатора  u_Cуст  соответствует q_уст. По соотношению (32) может быть определена емкость C_уст условно-линейного конденсатора. Для цепи (рис.17) в условно-линейном представлении постоянная времени переходного процесса t_уст  определяется соотношением

.

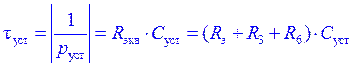В качестве временного интервала Dt при численном расчете переходного процесса рекомендуется выбирать отрезок времени длительностью не менеее 0,5t_уст.

ЛИТЕРАТУРА

1.  Зевеке Г.В., Ионкин П.А. Основы теории цепей.- М.: Энергия, 1989. 

2.  Атабеков Г.И. Линейные электрические цепи.-М.:Энергия,1978, ч I

3.  Бессонов Л.А. Теоретические основы электротехники. -М.: Высшая школа, 1973, ч.5.

4.  Ионкин П.А. Теоретические основы электротехники.- М.: Высшая школа, 1976, тI.

5.  Каплянский А.Е. Теоретические основы электротехники.-М.: Высшая школа, 1972.

6.  Нейман Л.Р., Демирчан К.С. Теоретические основы электротехники. -М.: Энергии, 1981, ч.2.

Приложение 1

ТИТУЛЬНЫЙ ЛИСТ

Министерство образования и науки РФ

Новосибирский государственный технический университет

Кафедра ТОЭ

Задание № ______     

___________________________________________________________

(название расчетно-графического задания)

Факультет__________________ Группа_____________________ Студент_____________________ Дата выполнения____________

Отметка о защите_____________________ Преподаватель________________________

Новосибирск _______