Алгоритмизированные задания по курсу ТОЭ. Анализ переходных процессов: Методическое руководство, страница 4

Докоммутационное напряжение на зажимах конденсатора может быть найдено из уравнения, составленного по второму закону Кирхгофа для любого из контуров, включающего в себя искомое напряжение (например, обозначенного пунктирной стрелкой)

 ,

где .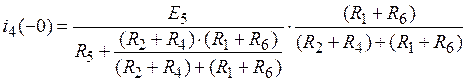

6. Определить зависимые начальные условия. Как известно, зависимыми начальными условиями называют все прочие начальные условия за исключением независимых. Для определения зависимых начальных условий для исходной схемы в послекоммутационном режиме следует составить полную систему уравнений Кирхгофа для мгновенных значений токов и напряжений. Ниже приведены эти уравнения в соответствии со схемой рис.6:

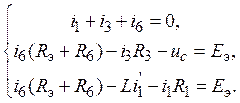                                                            (12)

Рассмотрим систему уравнений (12)для момента времени t = 0

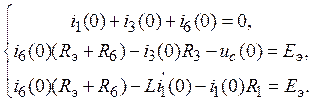                                                    (13)

Принимая во внимание, что независимые начальные условия i₁(0) и u_c(0) уже известны (см.пункт 5), в системе уравнений (13) остаются лишь три неизвестных, которые легко определяются. В частности, находится величина i₆(0).представляющая собой левую часть уравнений (5) и (6). Для определения левой части уравнений (9) и (10) необходимо систему уравнений (12) продифференцировать. В результате чего для t = 0 получим

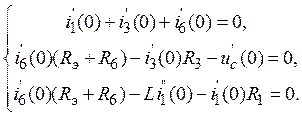                                                    (14)

Совместное решение систем уравнений (13) и (14) с учетом того, что

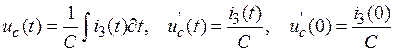                                                 (16)

позволяет определить производную искомой величины в начальный момент переходного процесса, в частности , представляющую собой левую часть уравнений (9) и (10).

Таким образом, совместное решение уравнений (5) и (9) для апериодического процесса или (6) и (10) для колебательного процесса позволит определить неизвестные A₁и A₂ или A и ψ, а затем, подставив их значения в уравнения (3) и (4), записать окончательные аналитические выражения для искомых переходных токов или напряжений.

Примечание. Если найден ток или напряжение на любом участке преобразованной цепи, с помощью первого и второго законов Кирхгофа можно определить токи и напряжения в любом участке исходной (непреобразованной) цепи.

1.4.2. Операторный метод

Если исходная схема (рис.1) после коммутации содержит три независимых контура, то ее рекомендуется преобразовать в двухконтурную (рис.6).

Пункт 2 задания предусматривает расчет переходного процесса в схеме операторным методом. В соответствии с конкретным примером пункта 2 карточки, переходный процесс имеет колебательный характер, а искомой величиной является переходный ток i₂ .

Рекомендуемый порядок расчета:

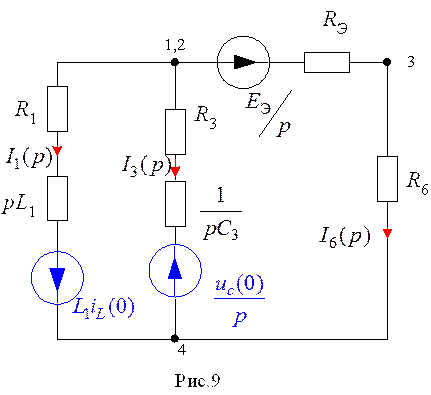
1.Составить эквивалентную операторную схему (рис.9) для цепи (рис.6) в послекомутационном режиме, используя операторные схемы замещения отдельных элементов (табл.2).

Таблица 2

Обратить внимание на выбранные положительные направления токов и внутренних операторных эдс  E_L(p) = L₁i_L(0) и  

2. Найти независимые начальные условия  i_L(0) и u_C(0), определяющие внутренние операторные эдс, используя законы коммутации. Этот пункт выполняется аналогично пункту 5 классического метода расчета.

 Примечание.  Принимая во внимание, что при расчете переходного процесса операторным методом в схеме изменяется по сравнению с исходной только значение емкости С, очевидно, что цифровые значения начальных условий i_L(0) и u_C (0), будут точно такими же, как и в классическом методе (см. пункт 5).

3. Рассчитать эквивалентную операторную схему (рис.9) любым из известных методов расчета цепей постоянного тока и найти требуемый операторный ток или операторное напряжение. Согласно пункту 2 карточки требуется определить ток i₂, протекающий по ветви с сопротивлением R₂ (рис.1). В операторной схеме (рис.9) ветвь с этим сопротивлением отсутствует, так как в результате преобразований R₂ вошло в R_Э. По схеме рис.9 можно определить операторное напряжение U₃₂(p), приложенное к сопротивлению R₂, а затем на основании закона Ома найти 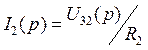, принимая во внимание, что операторная схема, до преобразования ее к двухконтурной, имела конфигурацию, показанную на рис.10.