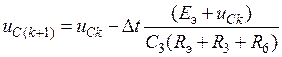Алгоритмизированные задания по курсу ТОЭ. Анализ переходных процессов: Методическое руководство, страница 7

,                                                 (24)

позволяющее рассчитать переходный процесс численным методом.

Порядок действий следующий.

В зависимости от требуемой точности расчета выбирается значение временного приращения Dt(см. примечание).

Для k = 0 уравнение (24) принимает вид

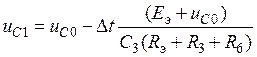,                                              (25)

где  - значение напряжения на конденсаторе в начале первого временного интервала Dt,  т.е. при t =0. С учетом закона коммутации

.

Как следует из схемы (рис.4), в установившемся докоммутационном режиме

.

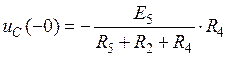Следовательно,

.

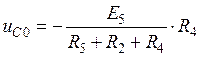Подставив найденное значение u_C0 в соотношение (25) можно определить u_C1, т.е. напряжение на конденсаторе в момент t = Dt.

Для k = 1 уравнение (24) принимает вид

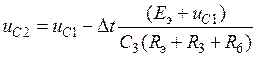,                                              (26)

где  - вышенайденное значение напряжения на конденсаторе в начале второго временного интервала Dt,  т.е. при t = Dt, а  определяемое значение напряжения на конденсаторе в конце второго временного интервала Dt,  т.е. при t = 2Dt. Далее, с помощью уравнения (24) определяются , , и т.д. Расчет ведется до тех пор, пока рассчитанные значения искомой величины в начале и конце очередного интервала не совпадут с требуемой точностью. Значения тока в любой рассматриваемый момент времени определяется из соотношения (21), представленного в соответствующей форме

.

по известным значениям напряжения на конденсаторе .

Результаты расчета целесообразно свести в таблицу 3

Таблица 3

Примечание. Практическая длительность переходного процесса составляет (4¸5)t, где t - постоянная времени переходного процесса. Для рассматриваемой цепи (рис.4)

.

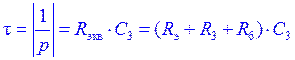В качестве временного интервала Dt при численном расчете переходного процесса рекомендуется выбирать отрезок времени длительностью не менеее 0,5t. При этом, анализ переходного режима будет проводиться с помощью не менее 8¸10 точек

1.4.6. Расчет переходного процесса в нелинейной цепи

В соответствии с пунктом 6 и данными карточки 1 задания исходная схема преобразовывается в схему рис.5, в которой емкость С₃ нелинейна (задана кулон-вольтной характеристикой q = f(u_C),где q – заряд конденсатора, u_C –напряжение на конденсаторе). Требуется определить напряжение u_C(t).

Переходные процессы в нелинейных цепях описываются нелинейными дифференциальными уравнениями. Существует достаточно много методов расчета переходных процессов в нелинейных цепях. Одним из наиболее эффективных методов является метод переменных состояния. В исследуемой цепи (рис.5) в качестве переменной состояния рассматривается заряд qконденсатора.

Если воспользоваться эквивалентной заменой резистивной части послекоммутационной схемы одной эквивалентной ветвью, то исходная схема (рис.5) для t > 0 может сведена к одноконтурной схеме, представленной на рис. 17.

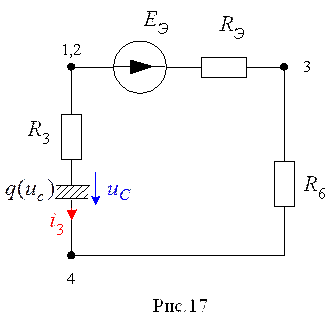Нелинейное дифференциальное уравнение, описывающее переходный процесс в цепи (рис.17) (с учетом того, что 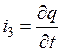), имеет вид:

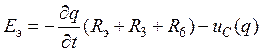                 (27)

В соотетствии с требованиями метода переменных состояния уравнение (27) может быть приведено к виду

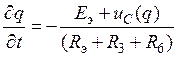.                                                              (28)

Нелинейное дифференциальное уравнение (28) может

быть представлено в конечно-разностной форме

,

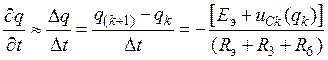или

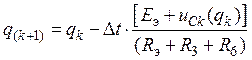                                                    (29)

Соотношение (29) позволяет рассчитать переходный процесс в рассматриваемой нелинейной цепи численным методом.

Порядок действий следующий.

В зависимости от требуемой точности расчета выбирается значение временного приращения Dt

(см. примечание)

Для k = 0 уравнение (29) принимает вид

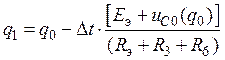,                                              (30)

где  - значение напряжения на конденсаторе в начале первого временного интервала Dt,  т.е. при t =0. С учетом закона коммутации