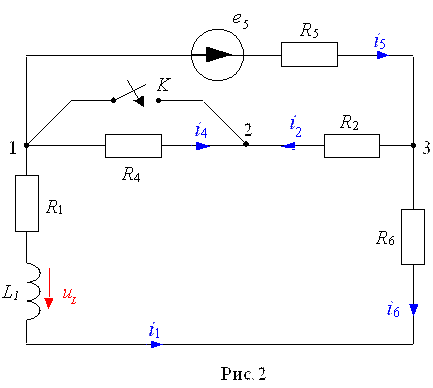
2. Рассчитать схему (рис.1) операторным методом (пункт 2 карточки) и определить значения указанного тока (напряжения). Значение емкости C взять соответствующее характеру заданного в данном пункте переходного процесса. Значение источника эдс E = const (то же, что и в пункте 1).
 |
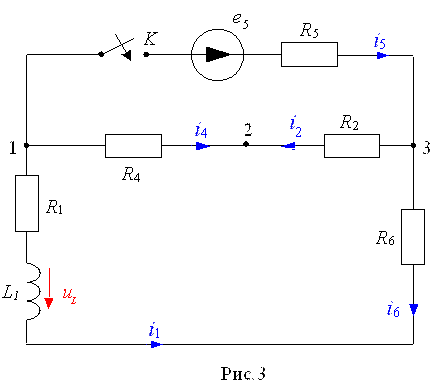
4. Рассчитать переходный процесс с помощью интеграла Дюамеля. При этом ключ переносится в ветвь с источником ЭДС и работает на включение. В соответствии с пунктом 4 задания один из реактивных элементов закорачивается, а вместо ЭДС E (рис.1) включается ЭДС e(t), график изменения во времени которой взять, в соответствии с карточкой, из рис. 1 ¸30.
 |
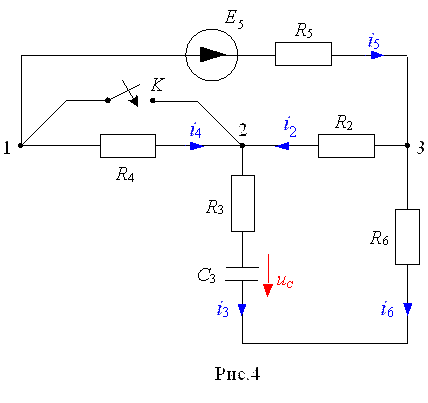
5. Рассчитать переходный процесс (ток в индуктивности или напряжение на емкости) методом переменных состояния. Значение источника ЭДС E = const и принимается тем же, что и в пунктах 1 и 2 задания. Расчетная схема к пункту 5 задания, в соот
 |
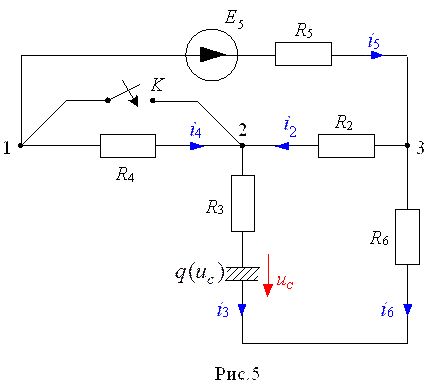
Примечание. Для пунктов 3, 4 и5 в случае, если в схеме остается емкость C, ее значение принимается равным CK.
 |


 К
резистивной части любой неоднородной цепи применимы методы преобразований,
известные из теории цепей постоянного тока. Поэтому, если имеется возможность,
послекоммутационную схему рекомендуется упростить, за счет сведения цепи, не
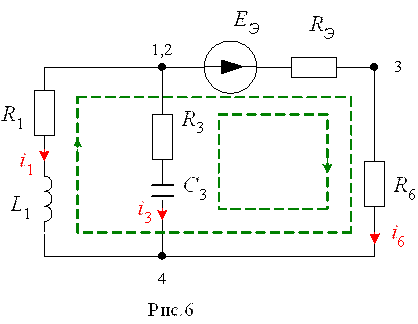
содержащей реактивных элементов, к одной эквивалентной ветви. Например, на рис.
1 показана исходная схема, в которой после коммутации (замыкания ключа)
сохраняется три контура. С учетом равнопотенциальности узлов 1 и 2 параллельные
резистивно-активные ветви (вторая и пятая) могут быть преобразованы в одну
эквивалентную активную ветвь с параметрами Eэ и Rэ. При
этом, послекоммутационная схема принимает вид, представленный на рис. 6.
Параметры эквивалентной ветви:
К
резистивной части любой неоднородной цепи применимы методы преобразований,
известные из теории цепей постоянного тока. Поэтому, если имеется возможность,
послекоммутационную схему рекомендуется упростить, за счет сведения цепи, не
содержащей реактивных элементов, к одной эквивалентной ветви. Например, на рис.
1 показана исходная схема, в которой после коммутации (замыкания ключа)
сохраняется три контура. С учетом равнопотенциальности узлов 1 и 2 параллельные
резистивно-активные ветви (вторая и пятая) могут быть преобразованы в одну
эквивалентную активную ветвь с параметрами Eэ и Rэ. При
этом, послекоммутационная схема принимает вид, представленный на рис. 6.
Параметры эквивалентной ветви:
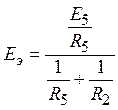 ,
, 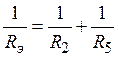 .
.
Первый пункт задания предусматривает расчет переходного процесса в схеме классическим методом. В соответствии с конкретным примером пункта 1 индивидуальной карточки переходный процесс имеет апериодический характер, а искомой величиной является переходный ток i6(t).
Рекомендуемый порядок расчета:
1. Записать общее решение для искомого тока (напряжения).
Например,
![]() (1)
(1)
 2.
Определить принужденную составляющую искомой величины. Для этого необходимо в
послекоммутационной схеме в установившемся режиме (t
= ∞) выполнить расчет i6пр любым
из известных методов расчета цепей постоянного тока. Так как в схеме (рис.6)
действует постоянная во времени ЭДС Eэ, то
2.
Определить принужденную составляющую искомой величины. Для этого необходимо в
послекоммутационной схеме в установившемся режиме (t
= ∞) выполнить расчет i6пр любым
из известных методов расчета цепей постоянного тока. Так как в схеме (рис.6)
действует постоянная во времени ЭДС Eэ, то 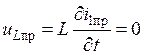 и
и 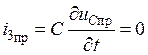 .
.
Расчетная схема для определения принужденных составляющих при Eэ = constпоказана на рис.7. Очевидно, что для рассматриваемой схемы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.