Алгоритмизированные задания по курсу ТОЭ. Анализ переходных процессов: Методическое руководство, страница 5

4. Перейти от операторных токов к оригиналам. Получить оригинал i₂(t) по изображению I₂(p) можно с помощью обратного преобразования Лапласа или с помощью справочных таблиц соответствия

при условии, что изображение может быть представлено в табличной форме. В большинстве случаев переход от операторных токов или напряжений к оригиналам осуществляется с помощью теоремы разложения в такой последовательности:

а) выражение I₂(p), полученное в пункте 3 привести к дроби вида

,

      где F₁(p) и F₂(p)есть степенные полиномы p,

б) представить полином знаменателя в виде F₂(p) = p(p² + Bp + Q)×A (множитель p перед скобкой может отсутствовать);

в) найти корни знаменателя, приравняв F₂(p) = 0.

Примечание. В случае, когда корни p₁ = 0;  p₂ < 0; p₃ < 0; p₁ ≠  p₂, в схеме имеет место апериодический переходный процесс. Если же корни p₁ = 0;p_2,3 = –a ± jω₀ , в схеме колебательный процесс. Наличие нулевого корня в составе знаменателя свидетельствует о существовании принужденной составляющей тока или напряжения.

г) записать теорему разложения для искомой функции

,

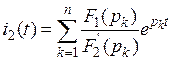где       n - высшая степень полинома F₂ (p);

                       .

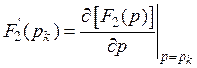В случае апериодического переходного процесса теорема разложения может быть записана как

.

         Если в составе полинома F₂(p) существуют комплексно-сопряженные корни, например, p_2,3 = –a ± jω₀ (колебательный переходный процесс), то в этом случае отпадает необходимость в непосредственном суммировании двух экспоненциальных функций и  где

,

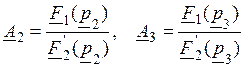 так как сумма их всегда будет равна удвоенному значению реальной части одной из них, т.е.

.

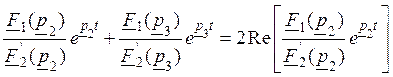5. Проверить полученное решение при t = 0 и при t = ∞. Для проверки рекомендуется использовать схему, характеризующую состояние рассматриваемой цепи в начальный момент

переходного процесса с учетом законов коммутации (рис.11) и схему (рис.12), определяющую установившийся режим. 

1.4.3. Классический метод расчета переходного процесса в цепи с синусоидальным источником питания

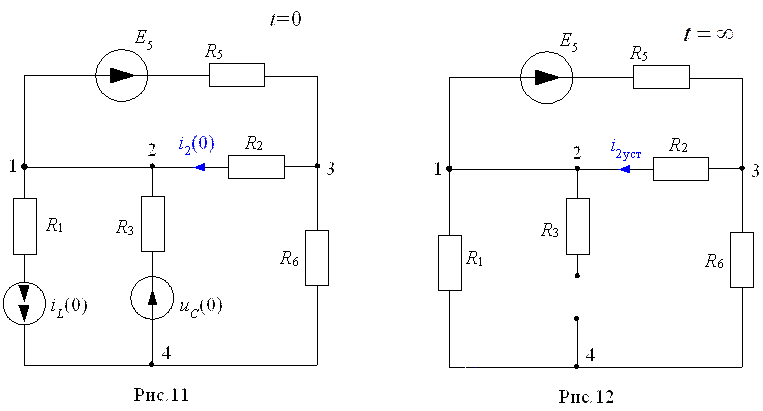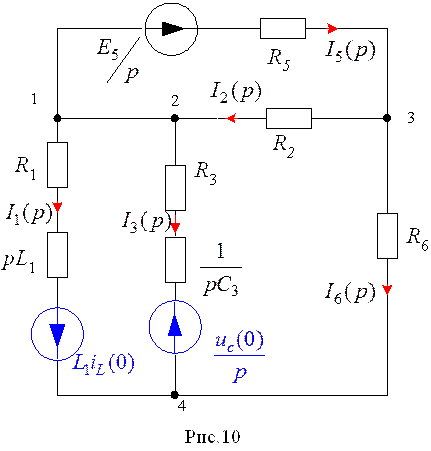
    В соответствии с пунктом 3 и данными карточки задания исходная схема преобразовывается

 в схему рис.2.

Рекомендуемый порядок расчета:

1.Записать искомую переходную величину (согласно карточке искомой величиной является ток i₁) в общем виде

i₁(t) = i_1пр(t) + i_1св(t).

 2. Определить принужденную составляющую искомой величины по схеме рис.2. Если воспользоваться эквивалентной заменой параллельных активно-резистивных ветвей (пятой и второй) в одну эквивалентную, послекоммутационная схема может быть приведена к одноконтурному виду (рис.13).

При этом параметры эквивалентной ветви определяются из соотношений:

,    ,

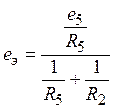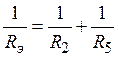где   .

Искомая величина в послекоммутационном установившемся режиме определяется символическим методом. В частности

.

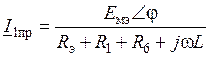Мгновенное значение принужденной составляющей искомой величины

i_1пр = I_1msin(ωt + φ₁).

3. С учетом того, что послекоммутационная схема (рис.13) содержит лишь один накопитель энергии, характеристическое уравнение для этой цепи будет иметь лишь один корень, определяемый соотношением

.

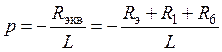В результате, свободная составляющая искомого тока будет иметь вид (см. табл.1):

,

а общее решение определится соотношением

.                                             (17)

Для определения постоянной А необходимо знать начальное значение (при t = 0) искомой переходной величины. Соотношение (17) для t = 0 имеет вид:

(18)

4. Определить независимое начальное условие i_L(0), используя закон коммутации, согласно которому i_L(0) = i_L(-0). Докоммутационная схема рассматриваемого режима представлена на рис. 14. Расчет установившегося докоммутационного режима (t < 0) проводится символическим методом. В частности,

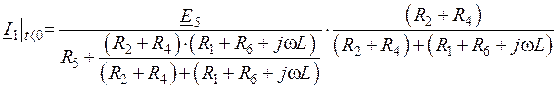.                      (19)

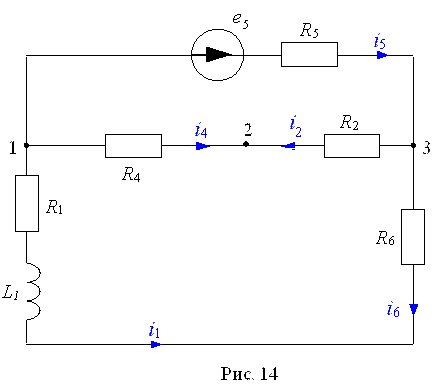Из соотношения (19) вытекает мгновенное значение докоммутационного установившегося тока в индуктивности

.        (20)

Из (20) следует

и, как следует из закона коммутации,

.

С учетом того, что   уравнение (18) может быть разрешено относительно  константы А.

1.4.4. Метод расчета переходного режима с помощью интеграла Дюамеля

В соответствии с пунктом 4 и данными карточки задания исходная схема преобразовывается в схему рис.3. При этом требуется определить переходный ток i₅(t).