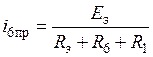 .
.
Если в соответствии с требованиями карточки задания требуется определить uCпр (напряжение в разрыве), достаточно составить уравнение по 2 закону Кирхгофа для любого контура, включающего искомое напряжение, например,
![]() ,
,
и найти uCпр после предварительного определения необходимых токов в ветвях.
3. Записать в общем виде выражение для свободной составляющей искомой величины. Для реализации пункта 3 следует иметь в виду, что в общем случае свободная составляющая представляет собой сумму слагаемых, число которых определяется числом корней характеристического уравнения, а вид этих слагаемых зависит от вида корней характеристического уравнения. Поэтому прежде всего следует составить характеристическое уравнение для послекоммутационной цепи и определить его корни.
Характеристическое уравнение можно получить, приравняв нулю главный определитель системы алгебраизированных уравнений, составленных по методу контурных токов для свободных составляющих в послекоммутационной схеме. Контуры рекомендуется выбирать так, чтобы в каждом из них было минимум реактивных элементов. Так, для схемы рис.6 (выбранные контуры обозначены пунктирными линиями) после представления индуктивного сопротивления как Lp, а емкостного как 1/pC, приравнивая нулю главный определитель системы уравнений, получим
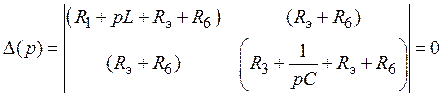
Это уравнение следует привести к виду
p2 + Bp + Q = 0 (2)
В случае, когда значение емкости взято из карточки для апериодического процесса (С = СА), в результате решения уравнения (2) должны получиться два действительных и различных корня p1 и p2. При этом p1 < 0, p2 < 0. Для колебательного процесса (когда С = СК) p1,2 = –a ± jω0 .
Аналитические выражения для свободных составляющих в зависимости от числа и харак-
тера корней характеристического уравнения представлены в таблице 1.
Таблица 1
|
№ п/п |
Число и характер корней |
Характер переходного процесса |
Вид свободной составляющей |
|
1 |
p1 < 0 |
Апериодический |
AeP1t |
|
2 |
p1 ≠ p2; p1 < 0; p2 < 0 |
Апериодический |
A1eP1t + A2eP2t |
|
3 |
p1,2 = –a ± jω0 |
Колебательный |
Ae–atsin (ω0 t + ψ) |
4. Записать общее решение для искомого тока (напряжения) с учетом известных корней характеристического уравнения.
Для апериодического процесса
![]() . (3)
. (3)
Для колебательного процесса
![]() . (4)
. (4)
С целью последующего
определения постоянных A1, A2 для апериодического
процесса и A,ψ для колебательного процесса необходимо найти
значение искомой функции ![]() и ее
производной
и ее
производной 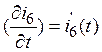 в начальный момент переходного
процесса, т.е. при t = 0.
в начальный момент переходного
процесса, т.е. при t = 0.
Запишем уравнения (3) и (4) для момента времени t = 0.
Для апериодического процесса
![]() .(5)
.(5)
Для колебательного процесса
![]() .
(6)
.
(6)
Дифференцируем выражение (3) или (4)
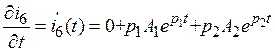 ,
(7)
,
(7)
или
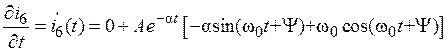 . (8)
. (8)
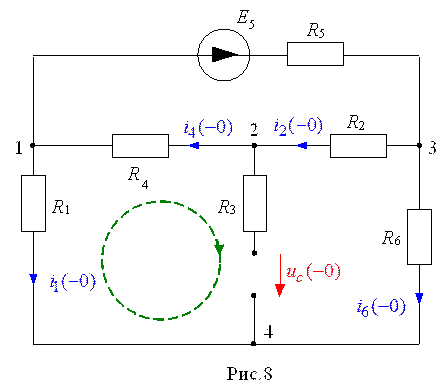
Рассматривая выражения (7) или(8) в момент времени t= 0 получим
![]() ,(9)
,(9)
или
![]() .
(10)
.
(10)
 Совместное решение
уравнений (5) и(9) для апериодического процесса, или (6) и(10) для колебательного процесса, позволит определить A1 и A2 или Aи ψ, если
будут известны левые частиi6 (0) и i'6 (0)этих уравнений,
которые носят названия начальных условий.
Совместное решение
уравнений (5) и(9) для апериодического процесса, или (6) и(10) для колебательного процесса, позволит определить A1 и A2 или Aи ψ, если
будут известны левые частиi6 (0) и i'6 (0)этих уравнений,
которые носят названия начальных условий.
5. Определить независимые начальные условия iL (0) и uC (0) с помощью законов коммутации, согласно которым
iL (0) = iL (– 0); uC (0) = uC (–0). (11)
Значения iL (0) и uC (0) могут быть найдены после расчета цепи в установившемся докоммутационном режиме (t < 0). Схема для расчета независимых начальных условий (c учетом E = const) показана на рис.8. Расчет этой цепи может проводиться с использованием любых методов расчета цепей постоянного тока. В частности, ток в индуктивности до коммутации
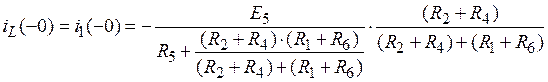 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.