Ознакомление с методикой приближенного представления функций в виде интерполяционного полинома и способами оценивания погрешностей интерполяции

Министерство образования Российской Федерации

Новосибирский государственный технический университет

Лабораторная работа №1

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

Вариант №6.

Выполнили:

Якименко А. А.

Григорьев В. В.

Крылысов А. В.

Группа: АП – 419

Факультет: АВТ

Проверил:

Соловьев

Новосибирск

2006 г.

1. Цель работы

Ознакомиться с методикой приближенного представления функций в виде интерполяционного полинома и способами оценивания погрешностей интерполяции.

2. Постановка задачи

Вычислить приближенные значения функции y = f(x),  x[a, b]  с шагом   (= 0,1) посредством интерполяционного полинома (n = 2, 3, 4), определенного через  в узлах интерполяции  (N = 3, 4, 5) с шагом   h = (b - a)/(N - 1) = const   на интервале [a, b].

      Оценить погрешности интерполирования функции y = f(x) на интервале [a, b].

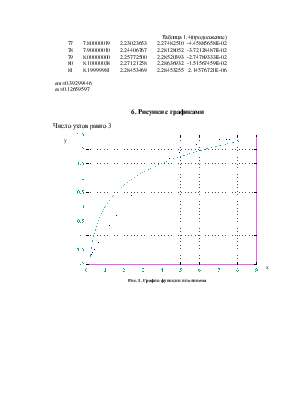
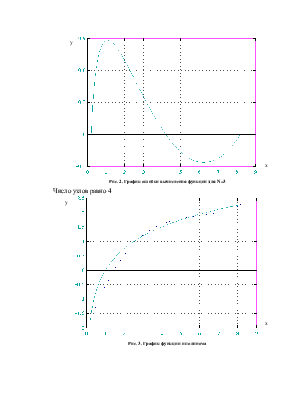
            Исследовать влияние количества узлов N (порядка n) на точность интерполирования.

Таблица 1.1

3. Краткие теоретические сведения

Формула интерполяционного полинома  в общем виде

Для построения графиков функций использовалась программа GRAPH (доступна на FTP сервере НГТУ кафедры АС: ftp://ac.cs.nstu.ru/pub/hell/work/wiymet/graph/), использующая выходные данные программы, приведенной в пункте 4.

4. Листинг программы на языке FORTRAN

      REAL FX(101),X(5),U(5,5),V(5),AK(5),XX(101),P(101),E(101)

      PRINT *,'N='

      READ *,N

      A=0.2

      B=8.2

      H=(B-A)/(N-1)

      DO 1 K=1,N

      X(K)=A+(K-1)*H

      FX(K)=2.5*alog10(X(K))

1     WRITE(1, 103) X(K), FX(K)

      CALL N1YSAU (N,X,FX,U,V)

      CALL N1YGAU (U,V,AK,N)

      DX=0.1

      KN=(B-A)/DX+1.1

      DO 2 K=1,KN

      XX(K)=A+(K-1)*DX

      FX(K)=2.5*alog10(XX(K))

      P(K)=0

      DO 2 I=1,N

2     P(K)=P(K)+AK(I)*XX(K)**(I-1)

      CALL N1YEEE (FX,P,KN,E,EM,ES,EP,EMO,ESO,EPO)

      DO 3 K=1,KN

3     WRITE (2,100) XX(K),FX(K),P(K),E(K)

      WRITE (2,101) EMO,ESO

      DO 4 K=1,N

4     WRITE (3,102) AK(K)

100   FORMAT (2X,3(1X,F9.4),1X,E11.4)

101   FORMAT (2X,'EMO=',E11.4,2X,'ESO=',E11.4)

102   FORMAT (2X, F9.4)

103   FORMAT (F9.4, F9.4)

      STOP

      END

5. Результаты вычислений

Таблица 1.2

0.20000    -1.74742

     2.20000     0.85606

     4.20000     1.55812

     6.20000     1.98098

     8.20000     2.28453

5.1.Коэффициенты полинома

Таблица 1.3

    -2.2184

     2.4831

    -0.6566

     0.0825

    -0.0038

Таблица 1.4

           k               x                      y=f(x)                 p(x)                 e(x)

           1       0.20000000      -1.74742496      -1.74742496   0.00000000E-01

           2       0.30000001      -1.30719686      -1.53040099       0.22320414

           3       0.40000001      -0.99484998      -1.32506549       0.33021551

           4       0.50000000      -0.75257498      -1.13095546       0.37838048

           5       0.60000002      -0.55462188      -0.94761634       0.39299446

           6       0.69999999      -0.38725489      -0.77460361       0.38734871

           7       0.80000001      -0.24227501      -0.61148119       0.36920619

           8       0.90000004      -0.11439371      -0.45782238       0.34342867

           9       1.00000000   1.61787295E-08      -0.31320974       0.31320977

          10       1.10000002       0.10348173      -0.17723492       0.28071666

          11       1.20000005       0.19795313  -4.94983196E-02       0.24745145

          12       1.30000007       0.28485841   7.03897849E-02       0.21446863

          13       1.39999998       0.36532012       0.18281059       0.18250953

          14       1.50000000       0.44022816       0.28813595       0.15209222

          15       1.60000002       0.51029998       0.38672838       0.12357160

          16       1.70000005       0.57612234       0.47894165   9.71806943E-02

          17       1.80000007       0.63818127       0.56512052   7.30607510E-02

          18       1.89999998       0.69688404       0.64559960   5.12844324E-02

          19       2.00000000       0.75257498       0.72070575   3.18692327E-02

          20       2.10000014       0.80554825       0.79075521   1.47930384E-02

          21       2.20000005       0.85605669       0.85605657   1.19209290E-07

          22       2.29999995       0.90431958       0.91690850  -1.25889182E-02

          23       2.40000010       0.95052814       0.97359991  -2.30717659E-02

          24       2.50000000       0.99485004       1.02641189  -3.15618515E-02

          25       2.60000014       1.03743339       1.07561553  -3.81821394E-02

          26       2.70000005       1.07840943       1.12147284  -4.30634022E-02

          27       2.79999995       1.11789513       1.16423750  -4.63423729E-02

          Таблица 1.4(продолжение)

          28       2.90000010       1.15599501       1.20415306  -4.81580496E-02

          29       3.00000000       1.19280314       1.24145412  -4.86509800E-02

          30       3.10000014       1.22840428       1.27636600  -4.79617119E-02

          31       3.20000005       1.26287496       1.30910575  -4.62307930E-02

          32       3.29999995       1.29628491       1.33988142  -4.35965061E-02

          33       3.40000010       1.32869732       1.36888862  -4.01912928E-02

          34       3.50000000       1.36017013       1.39632070  -3.61505747E-02