Решение дифференциального уравнения методом Адамса четвертого порядка точности

1.  Постановка задачи:

   На интервале  решить дифференциальное уравнение

   

            

с шагом методом Адамса четвертого порядка точности с прогнозом и коррекцией решения.

   Определить на  погрешности численной процедуры метода Адамса, для чего необходимо сравнить полученное решение  с точным , , вычисленным аналитически.  Уравнение второго порядка с правой частью  имеет решение

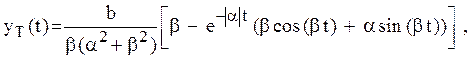
где  и  - вещественная и мнимая части корней характеристического уравнения

        

            Проанализировать влияние шага  решения дифференциального уравнения на точность решения, для чего необходимо изменить параметр  от  до c шагом

T		k
0,5	0,0	50,0	[0;   12]	0,05	0,09	0,01

3.  Текст программы:

          real eps,k,dt,y0(3),ak(3),a,b,y(3,450),f(450),y1(450),t1

      real ee(450),em,es,ep,emo,epo,x(450)

      integer i,l,kon,tp

      character V(5)

      data v/'1','2','3','4','5'/

      t=0.5

      eps=0.0

      k=50.0

      tp=12.

      dt=0.05

      hdt=0.01

      y0(1)=0

      y0(2)=0

      y0(3)=0

      ak(1)=1.0/(t*t)

      ak(2)=2*eps/t

      ak(3)=1

      a=ak(2)/2

      b=sqrt(abs(ak(2)*ak(2)-4*ak(1)))/2

      open(unit=7,file='E')

      write(7,*)'     DT      EMO      ESO'

      do 1 l=1,5

       kon=tp/dt+1.1

       t1=0

       do 2 i=1,kon

       f(i)=k*(b-exp(-a*t1)*(b*cos(b*t1)+a*sin(b*t1)))/(b*(b*b+a*a))

       t1=t1+dt

2      x(i)=1

       call n1ydua(2,3,ak,k,yo,dt,kon,x,y)

       do 3 i=1,kon

3      y1(i)=y(1,i)

       call n1yeee(f,y1,kon,ee,em,es,ep,emo,eso,epo)

       open(unit=8,file=v(l))

       write(8,*) '     T1           F(I)          Y1(I)         EE(I)'

       t1=0

       do 4 i=1,kon

        write(8,100) t1,f(i),y1(i),ee(i)

4      t1=t1+dt

       write(7,101) dt,emo,eso

1     dt=dt+hdt

100   format(2x,f8.4,3(f14.8))

101   format(2x,f7.3,2(f10.6))

      END

4.  Графики:

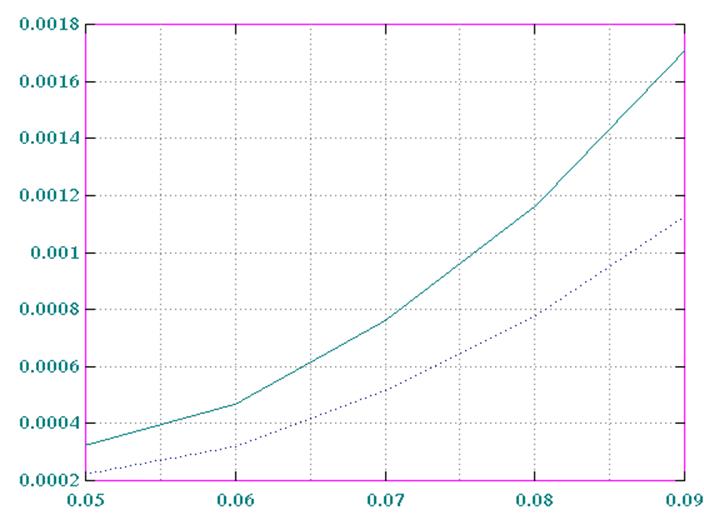
Рис. 1 Emo(DT), Eco(DT)

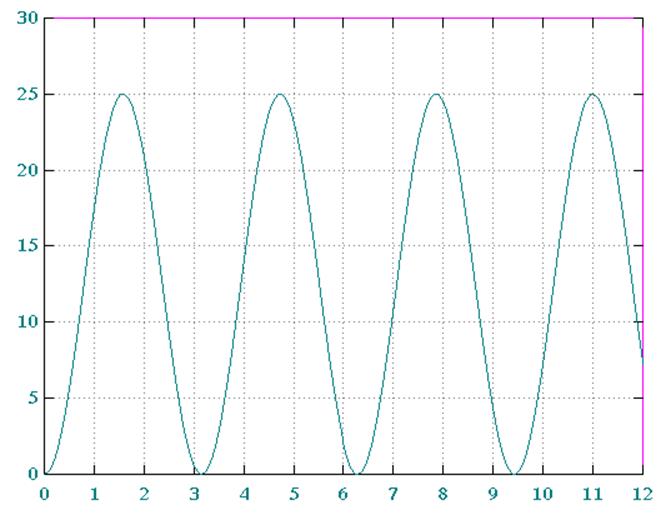
Рис.2y(t)

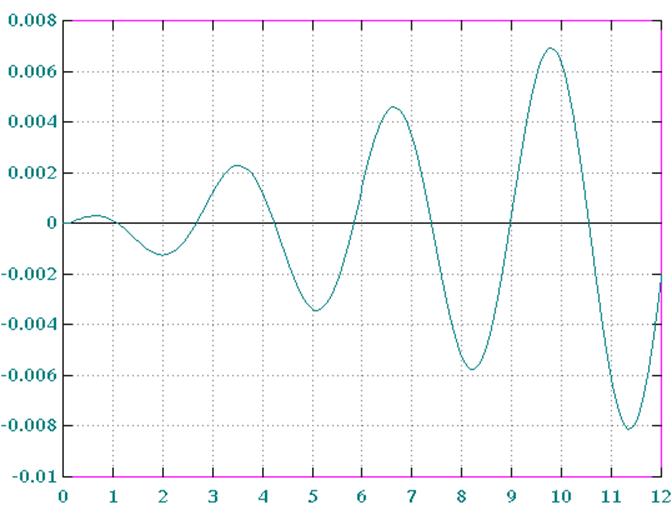
Рис. 3 Е(t) при DT=0.05

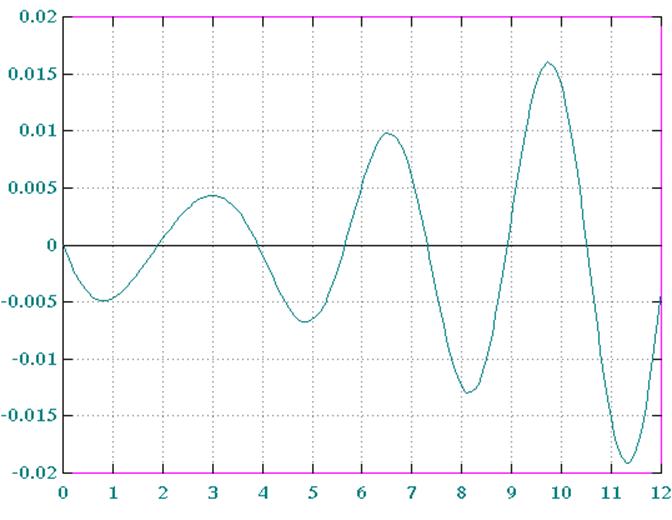
Рис. 4 Е(t) при DT=0.07

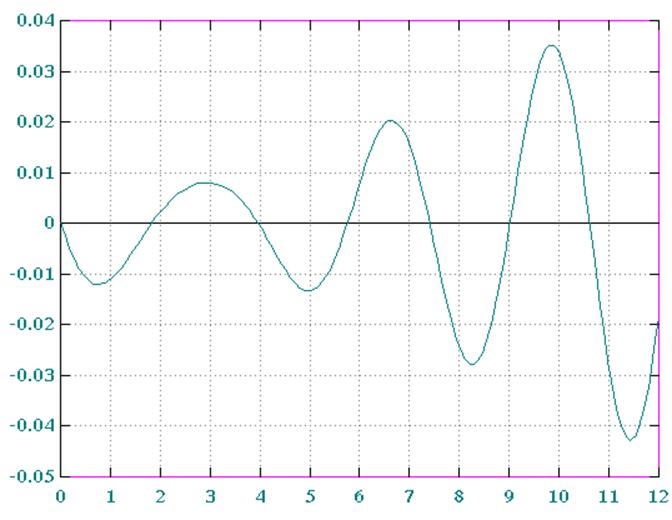
Рис. 5 Е(t) при DT=0.09

Вывод: