Практика использования итерационных методов решения системы линейных алгебраических уравнений

Министерство образования Российской Федерации

Новосибирский государственный технический университет

Лабораторная работа №3

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Вариант №6.

Выполнили:

Якименко А. А.

Григорьев В. В.

Крылысов А. В.

Группа: АП – 419

Факультет: АВТ

Проверил:

Соловьев

Новосибирск

2006 г.

1. Цель работы

            Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.

2. Постановка задачи

            Решить систему линейных алгебраических уравнений (САУ)

,   ,   ,    

итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.

Таблица 1.1

3. Краткие теоретические сведения

Методы решения САУ подразделяются на прямые (точные) и итерационные (приближенные). Прямые методы позволяют получить точное решение за конечное число арифметических операций. Наибольшее применение среди прямых методов получил метод Гаусса.

          Итерационные методы за конечное число итераций позволяют получать искомое решение с некоторой погрешностью e. Ниже приведены алгоритмы Зейделя и наискорейшего спуска, используемые в работе для решения САУ вида

,

        

          Метод Зейделя

           

 

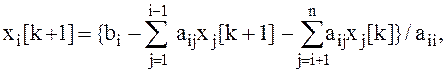
где  - i-я компонента вектора x на k-й итерации, , i[1, n] - начальные условия, которые рекомендуется задавать в виде , i[1, n].

          Метод Зейделя будет сходиться к единственному решению при выполнении условия

 ,   .

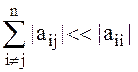          Метод наискорейшего спуска

,   ,

,   k = 0, 1, ... ,

,      ,

                    

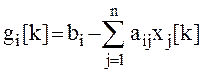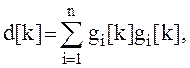
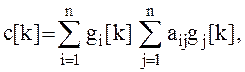
где - i-я компонента вектора  x  на  k-й  итерации, , i[1, n] - начальные условия, которые задаются, например, в виде = 0, i[1, n].

          Метод наискорейшего спуска сходится к единственному решению, если матрица A - симметрическая, положительно определенная.

          В общем случае для неособенной матрицы A можно предусмотреть условие сходимости метода путем первой трансформации Гаусса исходной САУ

,

где матрица - симметрическая, положительно определенная.

Для построения графиков функций использовалась программа WinGraph (доступна на FTP сервере НГТУ кафедры АС: ftp://ac.cs.nstu.ru/pub/hell/work/wiymet/graph/), использующая выходные данные программы, приведенной в пункте 4.

4. Листинг программы на языке FORTRAN

      subroutine slau (a, b, x,n, stype, xtype, fnum)

      integer fnum,stype,xtype

      dimension a(n,n),b(n),x(n),g(5)

      ep=0.001

      if(xtype.eq.1) goto 21

      if(xtype.eq.2) goto 22

21    do 211 i=1,n

211     x(i)=0

      goto 31

22    do 221 i=1,n

221   x(i)=b(i)/a(i,i)

31    k=0

      write(fnum,*)k,(x(i),i=1,n)

36    if(stype.eq.1) goto 11

      if(stype.eq.2) goto 12

11    call n1ymgs(a,b,n,g,x)

      goto 32

12    call n1ymns(a,b,n,g,x)

32    k=k+1

      write(fnum,*)k,(x(i),i=1,n)

      gm=abs(g(1))

      do 33 it=1,n

      if (gm.lt.abs(g(it))) gm=abs(g(it))

33     continue

      if(gm.gt.ep) goto 36

      return

      end

      real a(5,5),b(5),x(5)

      data a/0.490,  0.000,-0.128, 0.090, 0.150,

     *       -0.030, 0.320, 0.000,-0.061, 0.020,

     *        0.010,-0.090, 0.580, 0.011, 0.035,

     *        0.030, 0.000,-0.073, 0.580, 0.000,

     *        0.020,-0.030, 0.145,-0.012, 0.420/

      data  b/0.964,1.279,-1.799,-4.971,2.153/

      n=5

      call slau(a,b,x,n,1,1,8)

      call slau(a,b,x,n,2,2,11)

      call slau(a,b,x,n,2,1,9)

      call slau(a,b,x,n,1,2,10)

      call n1ygau (a,b,x,n)

      k=0

      write (12,*)k,(x(i),i=1,n)

      stop

      end

5. Результаты вычислений

Таблица 1.2