35 3.60000014 1.39075625 1.42235279 -3.15965414E-02
36 3.70000005 1.42050433 1.44715822 -2.66538858E-02
37 3.79999995 1.44945896 1.47089887 -2.14399099E-02
38 3.90000010 1.47766149 1.49372768 -1.60661936E-02
39 4.00000000 1.50514996 1.51578581 -1.06358528E-02
40 4.09999990 1.53195965 1.53720880 -5.24914265E-03
41 4.20000029 1.55812323 1.55812156 1.66893005E-06
42 4.30000019 1.58367121 1.57864058 5.03063202E-03
43 4.40000010 1.60863173 1.59887314 9.75859165E-03
44 4.50000000 1.63303125 1.61891496 1.41162872E-02
45 4.59999990 1.65689456 1.63885677 1.80377960E-02
46 4.70000029 1.68024468 1.65877545 2.14692354E-02
47 4.80000019 1.70310307 1.67874312 2.43599415E-02
48 4.90000010 1.72549021 1.69882059 2.66696215E-02
49 5.00000000 1.74742508 1.71905971 2.83653736E-02
50 5.09999990 1.76892543 1.73950291 2.94225216E-02
51 5.20000029 1.79000843 1.76018476 2.98236609E-02
52 5.30000019 1.81068969 1.78112841 2.95612812E-02
53 5.40000010 1.83098447 1.80235100 2.86334753E-02
54 5.50000000 1.85090673 1.82385850 2.70482302E-02
55 5.59999990 1.87047005 1.84564614 2.48239040E-02
56 5.70000029 1.88968718 1.86770344 2.19837427E-02
57 5.80000019 1.90857005 1.89001131 1.85587406E-02
58 5.90000010 1.92713010 1.91253424 1.45958662E-02
59 6.00000000 1.94537818 1.93523932 1.01388693E-02
60 6.09999990 1.96332455 1.95807171 5.25283813E-03
61 6.20000029 1.98097920 1.98097706 2.14576721E-06
62 6.30000019 1.99835134 2.00388908 -5.53774834E-03
63 6.40000010 2.01545000 2.02673006 -1.12800598E-02
64 6.50000000 2.03228331 2.04941463 -1.71313286E-02
65 6.59999990 2.04885983 2.07185316 -2.29933262E-02
66 6.70000029 2.06518698 2.09393549 -2.87485123E-02
67 6.80000019 2.08127236 2.11555004 -3.42776775E-02
68 6.90000010 2.09712267 2.13658333 -3.94606590E-02
69 7.00000000 2.11274505 2.15689659 -4.41515446E-02
70 7.09999990 2.12814593 2.17634678 -4.82008457E-02
71 7.20000029 2.14333129 2.19479465 -5.14633656E-02
72 7.30000019 2.15830708 2.21207619 -5.37691116E-02
73 7.40000010 2.17307925 2.22802162 -5.49423695E-02
74 7.50000000 2.18765306 2.24246216 -5.48090935E-02
75 7.59999990 2.20203400 2.25520611 -5.31721115E-02
76 7.70000029 2.21622682 2.26606178 -4.98349667E-02
Таблица 1.4(продолжение)
77 7.80000019 2.23023653 2.27482510 -4.45885658E-02
78 7.90000010 2.24406767 2.28128052 -3.72128487E-02
79 8.00000000 2.25772500 2.28520393 -2.74789333E-02
80 8.10000038 2.27121258 2.28636932 -1.51567459E-02
81 8.19999981 2.28453469 2.28453255 2.14576721E-06
em=0.39299446
es=0.12659597
|
|
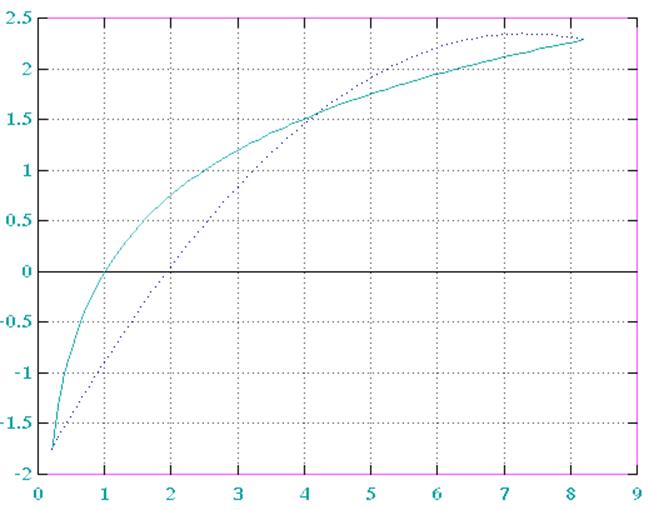
Рис. 1. График функции и полинома
|
|
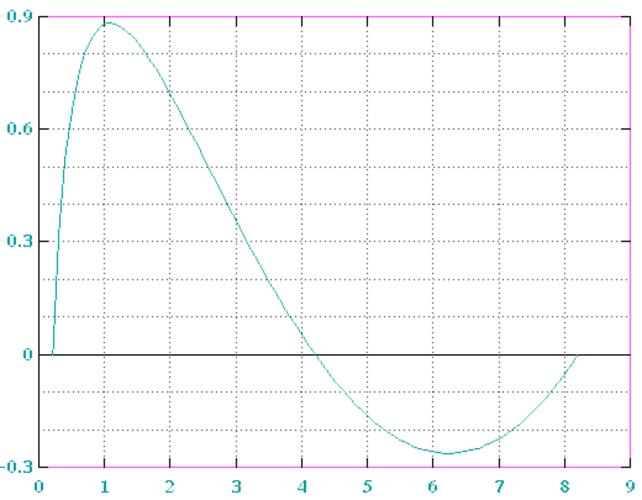
Рис. 2. График ошибки вычисления функции для N=3
|
|
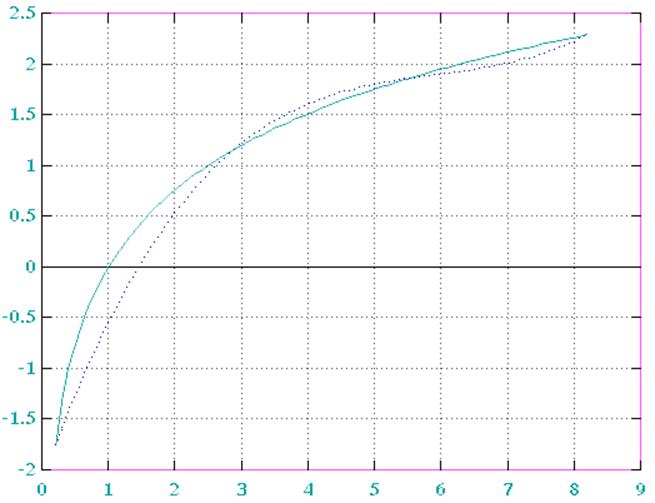
Рис. 3. График функции и полинома
|
|
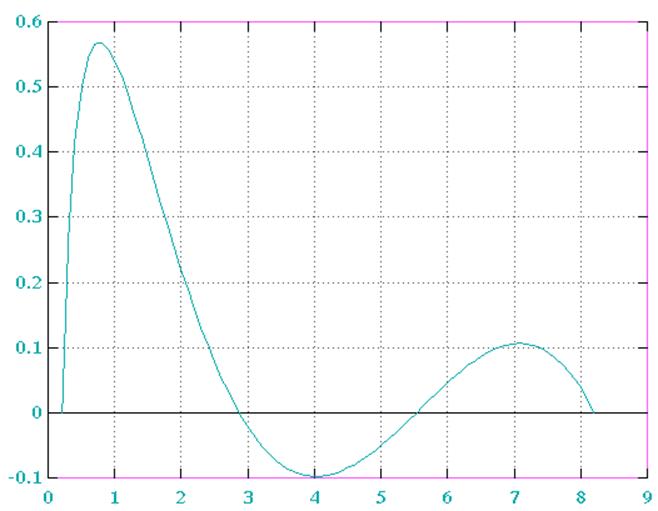
Рис. 4. График ошибки вычисления функции для N=4
|
|
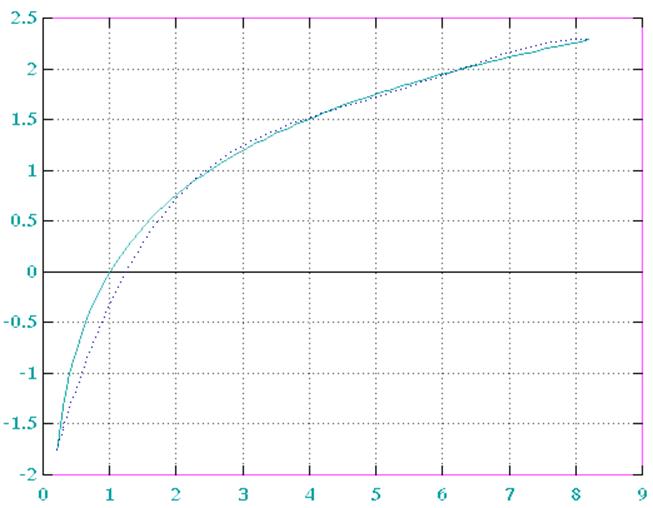
Рис. 5. График функции и полинома
|
|
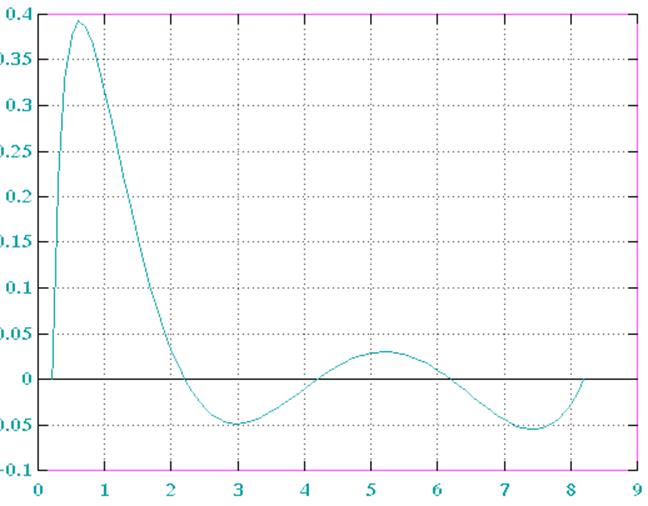
Рис. 6. График ошибки вычисления функции для N=5
На основании проделанного вычислительного эксперимента установили, что при увеличении количества узлов интерполяции методическая погрешность уменьшается. При числе узлов N=100, графики функций практически совпадают. По-видимому, при дальнейшем увеличении количества узлов совпадение будет ощутимо и при более детальной визуализации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.