Полином Лагранжа. Решение уравнения методом Ньютона. Решение систем линейных алгебраических уравнений

Полином Лагранжа

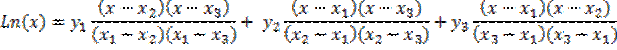
Полином Ньютона

По таблице опред Шаг h;    x – задан, по нему опред. I или II формула. Составляем новую таблицу изменения значений. Считаем t = (x-xn)/h

Если х ближе к левому краю то              Pn(x)=y0 + t*∆y0 + (t(t-1)/2!)∆²y0  +…

Если ближе к правому то                          P3(x)=y2 + t*∆y1 + (t(t-1)/2!) ∆2y0

Решение уравнения методом Ньютона

Выберем  х0 – начальное условие. Проверка на условие 1 f(x0)*f’’(x0)>0.(Только для нач. условий)

После проверка на условие 2 |f(x)*f’’(x)|< f²(x)/2     (Для всех х включая нач. условия)

Итерации происходят по формуле х1=х0 – f(x0)/f ’(x0); Проверка f(x)> ε и условие 2.

Решение систем линейных алгебраических  уравнений

a11x1 + a12x2 + a13x3 = b1         β1=b1/a11;                       x1 = β1 + α12x2 + α13x3

a21x1 + a22x2 + a23x3 = b2                                         =>       x2 = α21x1 + β2 + α23x3

a31x1 + a32x2 + a33x3 = b3         α12= - a12/a11                x3 = α31x1 + α32x2 + β3

Нач.Условия     х1(0)=β1;            x2(0)=β2;           x3(0)=β3.

1)Метод простых итераций

x1(1) = β1 + α12x2(0) + α13x3(0) Подставляя начальные условия получим 3 занчения х(1)

x2(1) = α21x1(0) + β2 + α23x3(0) <=Повторяем операцию с новыми условиями

x3(1) = α31x1(0) + α32x2(0) + β3

2)Метод Зейделя

x1(1) = β1 + α12x2(0) + α13x3(0) Подставляя начальные условия в первое уравнение находим

x2(1) = α21x1(1) + β2 + α23x3(0) х1(1) и подставляем во второе. Затем х2(1) подставляем в 3-е

x3(1) = α31x1(1) + α32x2(1) + β3 откуда получаем х3(1).