7.1. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
Функция f(x), определенная в некоторой окрестности точки x0, называется непрерывной в точке x0, если в этой точке существует конечный предел функции и он равен значению функции в этой точке:
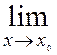 f(x)
= f(x0).
f(x)
= f(x0).
Пусть функция f(x) определена в некоторой окрестности точки x0. Для произвольной точки х из этой окрестности рассмотрим разность
Dх = х – х0
и назовем ее приращением аргумента в точке х0. Соответ-ствующую разность значений функции
Df(x0)= f(x) - f(x0) = f(x0+Dх) - f(x0))
назовем приращением функции f(x) в точке х0, соответствующим приращению аргумента Dх.
Рассмотрим основные свойства функции, непрерывной в точке.
С в о й с т в о 1 (приращение непрерывной функции). Для того чтобы функция, определенная в окрестности некоторой точки, была непрерывна в этой точке, необходимо и достаточно, чтобы бесконечно малому приращению аргумента соответствовало бесконечно малое приращение функции.
Это утверждение следует из равносильности двух предельных равенств:
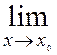 f(x)
= f(x0)Û
f(x)
= f(x0)Û ![]() Df(x0) = 0.
Df(x0) = 0.
Это свойство позволяет дать иное определение непрерывности функции в точке, равносильное первому.
Второе определение непрерывности функции в точке
Функция называется непрерывной в точке, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке:
![]() Df(x0)
= 0.
Df(x0)
= 0.
С в о й с т в о 2 (ограниченность непрерывной функции).
Если функция непрерывна в точке, то она ограничена в некоторой окрестности этой точки.
Доказательство следует из ограниченности функции, имеющей конечный предел.
С в о й с т в о 3 (сохранение знака непрерывной функ-ции). Если функция непрерывна в точке и имеет в этой точке значение, отличное от нуля, то существует такая окрестность точки, в которой функция сохраняет свой знак.
Доказательство. Пусть для определенности f(x0) > 0. В силу непрерывности
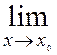 f(x)
= f(x0).
f(x)
= f(x0).
В соответствии с определением предела (п.5.1) это означает, что
"e>0 $d(e)>0: (х Î Ud(x0) Þ êf(x)- f(x0) ê< e).
Выбирая e достаточно малым (можно положить, например, e=1/2 f(x0)) и замечая, что
êf(x)- f(x0) ê< e Û f(x0) - e < f(x)< f(x0)+ e,
получаем, что для х Î Ud(x0) справедливо
f(x0) - e < f(x),
При выбранном e
f(x) > 0,5 f(x0) > 0,
т.е. в каждой точке d-окрестности точки х0 значения функции f(x) положительны, что и требовалось доказать. Аналогично проводится доказательство для случая, когда f(x0) < 0.
С в о й с т в о 4 (операции над непрерывными функциями). Если функции f(x) и g(x) непрерывны в точке x0, то функции
f(x) + g(x), f(x) × g(x), f(x) / g(x)
непрерывны в этой точке, последняя (частное) при условии, что f(x0) ¹ 0.
Доказательство следует непосредственно из теоремы об арифметических операциях над функциями, имеющими конечный предел.
Напомним, что каждая элементарная функция непре-рывна в каждой внутренней точке множества, на котором она определена.
7.2. ТОЧКИ РАЗРЫВА ФУНКЦИИ
Рассмотрим функцию, которая определена в окрестности точки х0 , кроме, может быть, самой этой точки.
О п р е д е л е н и е 1. Точка х0 называется точкой разрыва функции f(x), если функция не определена в этой точке или если функция определена в ней, но не является непрерывной.
О п р е д е л е н и е 2. Точка разрыва функции f(x)называется точкой разрыва 1 рода (или точкой конечного разрыва), если в ней существуют конечные односторонние пределы f(x0-0), f(x0+0). В противном случае - точкой разрыва 2 рода.
О п р е д е л е н и е 3. Разность f(x0+0) - f(x0-0) одно-сторонних пределов функции в точке разрыва 1 рода называется скачком функции f(x) в этой точке.
О п р е д е л е н и е 4. Точка разрыва 1 рода называется точкой устранимого разрыва, если в ней скачок равен нулю, т.е. f(x0+0) = f(x0-0).
П р и м е р 1. Функция
f(x)
= 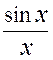
в точке x0 = 0имеет устранимый разрыв, т.к. в этой точке функция не определена, имеет в этой точке предел, равный 1 (п.5.8), и, следовательно, ее скачок в этой точке равен нулю.
П р и м е р 2. Функция
f(x)
= 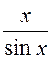
имеет разрывы во всех токах x = kp, где k - целое число, потому что в каждой такой точке функция не определена. В точке x = 0 устранимый разрыв, в каждой точке x = kp, где k - целое число и не равно нулю, - разрыв 2 рода, т.к. в этих точках не существует односторонних конечных пределов.
П р и м е р 3. Функция
f(x) = [x],
где [x] - целая часть числа х, имеет разрыв 1 рода в каждой точке х = k, k - целое. Скачок функции в каждой такой функции равен 1, кроме точки х = 0. В этой точке скачок равен 2.
7.3. СВОЙСТВА ФУНКЦИИ,
НЕПРЕРЫВНОЙ НА ОТРЕЗКЕ
О п р е д е л е н и е . Функция f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.
Обозначение: f(x) Î C(X). Здесь C(X) - класс функций, непрерывных на множестве Х.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.