Непрерывность функции в точке. Точки разрыва функции. Свойства функции, непрерывной на отрезке. Непрерывность функции нескольких переменных, страница 3

"e>0  $d(e, x₀)>0:  (х Î U_d(x₀)  Þ  êf(x)- f(x₀) ê< e).

      Иначе говоря, при заданном e различным точкам x₀  соответствуют, вообще говоря, различные значения d. Нас будет интересовать ситуация, когда для всех точек x₀ можно указать одно значение d. В этом случае мы будем говорть, что функция f(x) равномерно непрерывна на множестве Х. Дадим теперь определение равномерной непрерывности функции.

      О п р е д е л е н и е. Функция f(x)  называется равномерно непрерывной на множестве Х, если для любого положительного числа e и для каждой точки х₀, х₀ Î Х, существует такое положительное, зависящее от e (и не зависящее от х₀!) число d, что для всех х из d-окрестности точки х₀ соответствующее значение функции f(x) содержится в e-окрестности точки  f(x₀).

" e > 0,  " x₀Î X   $ d(e) > 0:  xÎU_d (x₀) Þ  f(x) Î U_e(x₀).

     Теорема Кантора.  Если функция f(x) непрерывна на отрезке [a,b], то она равномерно непрерывна на этом отрезке.

      Доказательство. Предположим противное: пусть непре-рывная на отрезке [a, b] функция f(x) не будет равномерно непрерывной на этом отрезке. Это означает, что существует такое положительное число e, что для всех d,  d > 0,  существуют такие две точки  x, на отрезке  [a, b], для которых  |f(x) -f()| ³ e.

     Рассмотрим  бесконечную числовую последовательность {d_n}, предел которой равен нулю:  d_n = 0. Можно положить, например,  d_n = 1/n. Для каждого d_n  выбираем соответствующую пару  x_n, x¢_n  такую,  для которой

| x_n – x¢_n | < d  Þ  |f(x_n) -f(x¢_n)| ³ e.                 (1)

      Из бесконечной последовательности {x_n} можно получить такую частичную бесконечную последовательность, которая имеет конечный предел х₀:

x_n =  х_0.

Ради простоты записи эту частичную последовательность обозначим так же: {x_n}.  Из непрерывности функции следует, что соответствующая последовательность {f(x_n)} имеет конечный предел  f(х₀):

 f(x_n)  =  f(х₀).

Это противоречит выбору членов последовательности:

| x_n – x¢_n | < d  Þ  |f(x_n) -f(x¢_n)| ³ e.

Противоречие доказывает теорему.

7.4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Непрерывность функции в точке

       Непрерывность функции нескольких переменных  определяется так  же, как и в одномерном случае.

      О п р е д е л е н и е.  Функция,  определенная  в  окрестности  точки  а, называется  непрерывной в этой точке, если в этой точке существует конечный предел функции и равен значению функции в этой точке:

                                         lim f(x) = f(a).                                       (4.2.1)

                                        x®a

      В этом случае говорят, что а - точка непрерывности функции f(x).

      Т е о р е м а .  Для того,  чтобы  функция   f(x)   была  непрерывна  в

  точке а, необходимо и достаточно, чтобы в этой точке были непрерыв-

  ны все ее координатные функции.

          Справедливость теоремы следует из теоремы п. 3.2.1 и определения непрерывности  функции в точке (4.2.1).

 Приращение непрерывной функции

         Рассмотрим функцию, которая определена в некоторой окрестности точки х₀:

y = f(x),  x Î U(x₀).

       Разность  Dx = x – x₀   называется приращением аргумента  в токе х₀. Разность  соответствующих значений функции называется приращением функции f(x) в точке х₀, соответствующим приращению аргумента Dx:

                Df(x₀) = f(x) – f(x₀) = f(x₀ + Dx) – f(x₀).               (4.3.1)

      Напоминаем, что как и в одномерном случае  [2], приращение данной функции в фиксированной точке х₀  есть функция, аргументом которой является приращение аргумента Dx.

     Приращение линейной функции  y = Ax  в каждой точке  x получаем по формуле (4.3.1)  и по правилам действий с матрицами:

Dy = A (x +Dx) – Ax = A Dx.

Короче:

y = AxÞDy= A Dx.

            Т е о р е м а . Для того, чтобы функция  f(x)  была непрерывной в точке х₀,  необходимо и достаточно, чтобы

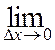                                        Df(x₀) = 0.                                     (4.3.2)                                            

Теорема доказывается так же, как и соответствующая теорема для числовой функции одного аргумента [2].

Свойства функции, непрерывной в замкнутом ограниченном множестве

      Функция, непрерывная в каждой точке множества, называется непрерывной в этом множестве. Нас здесь будет интересовать функция. непрерывная в замкнутом ограниченном множестве (т.е. на компакте). Такая функция обладает свойствами, аналогичными свойствам числовой функции, непрерывной на отрезке [Л.2].  Мы приведем формулировки этих свойств для числовой функции нескольких переменных.

      С в о й с т в о  1. Функция, непрерывная на компакте, ограничена в этом множестве.

      С в о й с т в о  2.  Функция, непрерывная на компакте, достигает в нем своего наименьшего и наибольшего значения.

      С в о й с т в о  3.   Функция, непрерывная на компкте, принимает в нем все возможные значения от наименьшего до наибольшего.