Рассмотрим свойства функции, непрерывной на отрезке: f(x)Î C([a,b]). Мы приведем формулировки основных теорем, устанавливающих свойства таких функций.
Первая теорема Коши. Если функция f(x) непрерывна на отрезке [a, b] и на границах отрезка принимает значения разных знаков, то существует точка внутри отрезка, в которой функция принимает значение, равное нулю.
(f(x) Î C[a, b] ) Ù (f(a) f(b)<0) Þ $ c Î[a, b] : f(c) = 0.
Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, в некоторой внутренней точке отрезка [a,b] пересекает ось абсцисс.
Доказательство. Отрезок [a, b] разобьем на два равных отрезка и выберем тот из двух, на границе которого функция принима6ет значения разных знаков. Обозначем его [a1, b1]. Повторяем деление пополам и выбор отрезка [an, bn]. Длина каждого из половинных отрезков равна bn- an = (b-a)/2n.
( bn- an)
= 0, [an, bn]É [an+1, bn+1].
Применима лемма о вложенных промежутках:
an = bn = с.
Однако для всех n f(an) ³ 0, f(bn) £ 0. По теореме о предельном переходе в неравенстве
f(an) ³ 0, f(bn) £ 0.
Отсюда следует
f(an) = f(bn) = 0.
В силу непрерывности функции
f(an) = f(an) = f(c) = 0,
что и требовалось доказать.
Вторая теорема Коши. Если функция f(x) непрерывна на отрезке [a,b] и на границах этого отрезка принимает различные значения f(a) = А, f(b) = В, А ¹ В, то для любого числа С между А и В, А < C < B (или В < C < A), то существует такая точка с, а < с < b, в которой функция принимает значение, равное С: f(c) = C.
Иначе говоря,
(f(x) Î C([a,b]), f(a) = А, f(b) = В, А ¹ В)) Þ
Þ ("С: ((A < C < B) Ú (A > C > B)) $c Î [a, b]: f(c) = C.
Доказательство. Для доказательства достаточно применить 1 теорему Коши для функции
g(x) = f(x) - C.
(f(x) Î C[a, b]) Ù (f(a) ¹ f(b)) Þ
Þ"C: f(a) < C < f(b) (или f(a)>C >f(b)) $c Î [a, b]: f(c) = C.
Доказательство. Для доказательства достаточно приме-нить первую теорему Коши для функции
g(x) = f(x) - C.
Теорема существования обратной функции. Если функция f(x) непрерывна на промежутке Х = (а, b) и строго монотонна на этом промежутке, то на множестве Y = f(X) существует обратная функция g(y), монотонная и непрерывная на этом множестве.
Доказательство. Для определенности пусть функция f(x) монотонно возрастает. Для любого у0 Î Y существует х0 Î Х, такое что у0 = f(x0). Такая точка х0 будет единственной, т. к. функция монотонна. В противном случае было бы у0 = f(x0) = f(x1), x0 ¹ x1, что невозможно.
Сопоставляя каждому у0 Î Y соответствующее х0 Î Х, получаем функцию обратную х = g(y).
Докажем, что эта функция монотонно возрастает. По условию
f(x0) < f(x1) Û x0 < x1,
а это означает, что
y0 < y1 Û g(y0) < g(y1),
т. е. обратная функция монотонна. Непрерывность обратной фнкции следует из второй теоремы Коши.
Первая теорема Вейерштрасса. Если функция f(x)непрерывна на отрезке [a,b], то она ограничена на этом отрезке.
Иначе говоря,
f(x)Î C([a,b]) Þ ($m, M: x Î [a,b] Þ m < f(x) < M).
Доказательство. От противного: пусть для любого n cуществует x = xn такое что f(xn) > n. Рассмотрим соответствующую бесконечную последовательность {xn}. Из нее можно получить частичную последовательность, имеющую конечный предел (теорема Больцано – Вейерштрасса, п.5.2):
= x0.
По непрерывности
f() = f(x0),
что противоречит построенной последовательности:
f() = +
¥.
Вторая теорема Вейерштрасса. Если функция f(x)непрерывна на отрезке [a,b], то она на этом отрезке достигает своего наибольшего и наименьшего значения.
В символической форме это можно записть так:
f(x) Î C([a,b]) Þ
Þ $ x1, x2Î [a,b]: (xÎ [a,b] Þ f(x1) £ f(x) £ f(x2).
Доказательство. Ограничимся доказательством утвер-ждения о наибольшем значении. Пусть М = sup{f(x)}. По определению точной верхней границы для любого n найдется такое x = xn на отрезке, что
f(xn) > M - 1/n.
Из последовательности {xn} можно извлечь частичную последовательность {}, сходящуюся к некоторому конечному пределу х0,
и по непрерывности
f() = f(x0).
Однако предельным переходом (n®¥) в неравенстве f(xn) > M - 1/n получаем
f(x0) ³ М.
Но М = sup{f(x)}, поэтому f(x0) = М, что и требовалось доказать.
7.4. РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Рассмотрим функцию f(x), непрерывную на множестве Х. В соответствии с определением непрерывности это означает, что для в каждой точке х0 существует конечный предел функции и он равен значению функции в этой точке:
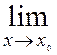f(x)
= f(x0).
Поэтому для любых e и х0, e > 0 и х0 Î Х, существует такое положительное, зависящее от e и х, число d = d(e, х0), что если только х оказывается в d-окрестности точки х0, то соответствующее значение функции f(x) обязательно попадает в e-окрестность конечной точки f(x0):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.