Дифференцируемость функции. Частное приращение, частный дифференциал и частная производная

4. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ

4.1. Общее определение дифференцируемости функции

      Напомним  сначала определение дифференцируемости числовой функции одного аргумента (второе определение дифференцируемости и производной [1]). Функция  у = f(x), которая определена в окрестности точки  х₀,  называется дифференцируемой в этой точке, если справедливо равенство

                              Df(x₀) = АDx + a(Dx) Dx,                              (4.1.1)

где  Dx - приращение аргумента, Df(x₀)  –  соответствующее приращение функции в точке х₀,  А – константа для данной функции и точки (не зависит от Dx), a(Dx) – бесконечно малая функция при бесконечно малом  Dx:  lim a(Dx) = 0,  Dx ® 0.

      Постоянная А в равенстве (4.1.1) называется производной функции  f(x) в точке х₀  и обозначается  f ¢(x₀).

      Как известно [5], равенство (4.1.1) равносильно такому определению производной:             

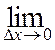
                              f ¢(x₀)   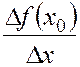  .                              (4.1.2)

      Рассмотрим теперь векторную функцию нескольких переменных  y = f(x), х Î X, y Î Y,  ХÌRⁿ, YÌR^m, которая определена в окрестности точки  х₀.

     Вводим обозначения:   

точка    x₀ =  (x₁₀,x₂₀, ... ,x_n0) ^T;

приращение аргумента     Dx = (Dx₁, Dx₂, ... , Dx_n)^T;

`

приращение функции     Df(x₀) = (Df₁(x₀) , Df₂(x₀) , ... , Df_m(x₀))^T;

бесконечно малая функцияa(Dx) = (a₁(Dx), a₂(Dx), ... , a_m(Dx)),

                             a_k(Dx) = 0,  Dx ®0,  k = 1,2, ... , m;          

матрица размера  m´n     А.

         О п р е д е л е н и е.  Функция  y = f(x),  х Î X,   y Î Y,   ХÌRⁿ,

YÌR^m, которая определена в окрестности точки х₀, называется дифференцируемой в этой точке, если существует матрица А размера m´n, которая не зависит отDx, и такая, что  справедливо равенство:

Df(x₀) = А Dx + a(Dx)Dx,                              (4.1.3)

      В этом случае матрица  А  называется матрицей-производной этой функции в точке  х₀.

      Cлучай    m = 1   соответствует числовой функции нескольких переменных,  n = 1  –  векторной функции скалярного аргумента,  m = n = 1 –  числовой функции числового аргумента.

       Равенство (4.1.3) означает, что с точностью до бесконечно малой a(Dx)Dx  приращение  функции  Df(x₀)  есть линейная функция приращения аргумента Dx. Иначе говоря, в окрестности точки дифференцируемости функция линейна с точностью до бесконечно малой высшего порядка (см. п.3.3):

В этом смысле говорят, что в формуле (4.1.3)  АDx есть главная линейная относительно Dxчасть приращения функции Df(x₀) в окрестности точки х₀.    

      О п р е д е л е н и е . Линейное относительно Dxслагаемое АDxв выражении (4.1.3) для дифференцируемой функции называется дифференциалом этой функции, точнее – полным дифференциалом. Обозначение – df(x₀):

                                        df(x₀) = А Dx.(4.1.4)

      Ясно, что если функция  дифференцируема в некоторой точке, то в окрестности этой точки справедливо

f(x)  = f(x₀)  + А (x – x₀)  + o(x– x₀).                 (4.1.5)

     Иначе говоря, дифференцируемая функция допускает приближенное линейное представление в окрестности точки ее дифференцируемости:

f(x)≈f(x₀)  + А (x – x₀),        xÎU(x₀).          (4.1.6)  

      Матричное равенство (4.1.3) равносильно следующей системе координатных равенств:

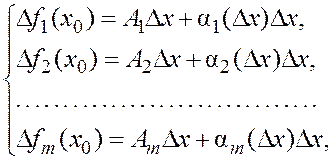                       (4.1.7) 

где  А_k  –  строчные матрицы размера  n,  k = 1, 2, ... , m.  Эти матрицы являются блоками, образующими матрицу А:

А =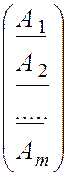 = 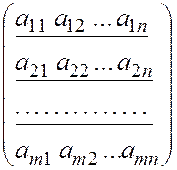.                     (4.1.8)

      Из равенств (4.1.3) и (4.1.7) следует справедливость следующего утверждения.

      Теорема.  Для  того,  чтобы  функция   y = f(x),  х Î X, y Î Y,  Х ÌRⁿ, YÌR^m,  была дифференцируемой в точке х₀, необходимо и достаточно, чтобы дифференцируемой в этой точке была каждая ее координатная функция.

      Нам предстоит выяснить, как вычисляются элементы матрицы-производной  А  для функции общего вида. Выясним вначале этот вопрос для ее координатных функций, которые являются числовыми функциями нескольких переменных.

4.2. Непрерывность дифференцируемой функции

Следующая теорема является обобщением теоремы о непрерывности дифференцируемой  числовой функции числового аргумента [2].

      Теорема.  Если функция нескольких переменных дифференцируема в точке, то она непрерывна в этой точке.

      Доказательство. Из определения дифференцируемости функции (п.4.1) следует, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции (4.1.3), а это, как следует из теоремы п.3.3, есть необходимое и достаточное условие непрерывности функции в точке.

      Обратное утверждение неверно. Чтобы убедиться в этом, достаточно вспомнить пример функции, непрерывной в точке, но не дифференцируемой  в этой точке [5].

4.3. Дифференцируемость числовой функции

нескольких переменных

      Дифференцируемость векторной функции нескольких переменных  в силу теоремы  п. 3.1 сводится к дифференцируемости всех ее координатных функций. Поэтому мы  перефразируем сейчас общее определение дифференцируемости функции  (п. 3.1, формула (3.1.3)) для случая  m = 1, т.е. для числовой функции.

      Числовая функция  u = f(x),xÎ X,X Ì Rⁿ, называется дифференцируемой в точке x₀, если  справедливо равенство