Дифференцируемость функции. Частное приращение, частный дифференциал и частная производная, страница 4

4.6. Производные высших порядков

      Частные производные функции нескольких переменных в произвольной точке   множества, где они определены,

,

в свою  очередь, являются функциями тех же переменных. В случае, если они дифференцируемы, можно определить, как и для функции одного аргумента,  их дифференциал и частную производную. Эти дифференциалы и производные называются соответственно дифференциалами и производными высших порядков.

Определим вначале частные производные высших порядков, для простоты ограничиваясь случаем функции двух переменных. Положим по определению

    

      .

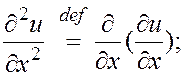
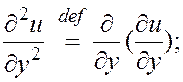
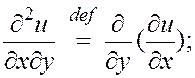
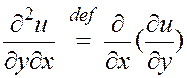      Производные, стоящие во второй строке, называются смешанными производными.

      Частные производные более высоких порядков определяются аналогично. Так, например,

.

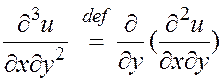Аналогично определяются частные производные третьего и вообще любого порядка для функции двух, трех и более переменных.

      Смысл обозначения 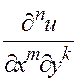    ,  где    ясен из предыдущего.

            П р и м е р ы.

1.  Для  функции  найти производную третьего порядка

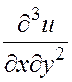      и вычислить ее значение в точке (1, 0). Последовательно

     дифференцируя функцию, получаем:

;    ;    .

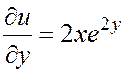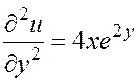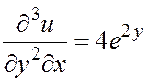     Для     значения   производной   в  точке  удобней  пользоваться

     другим обозначением:

.

2.  Находим  все  частные  производные  второго  порядка функции

     . Для этого найдем вначале частные производные первого

     порядка:

,   .

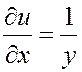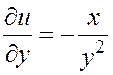     Теперь в соответствии с определением получаем:

  ;      .

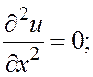
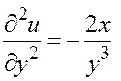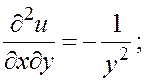
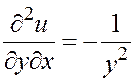      Замечаем, что смешанные производные не зависят от последовательности  дифференцирования:

.

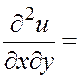
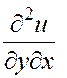      Это имеет место для всех смешанных производных функций нескольких переменных. Справедлива следующая теорема.

      Теорема. Если смешанные производные непрерывны в окрестности некоторой точки, то значение их в этой точке не зависит от последовательности  дифференцирования.

      Несложное доказательство этой теоремы для рассмотренного здесь случая  смешанных производных второго порядка предлагаем провести самостоятельно. Указание: воспользоваться формулой конечных приращений [1],[5].

4.7. Дифференциалы высших порядков

 Ради простоты записи формул определение дифференциалов высших порядков приведем для функции двух переменных.

       Предположим, что функция   имеет непрерывные частные производные до второго порядка в окрестности точки  где обе координаты есть независимые переменные. Тогда полный дифференциал ее

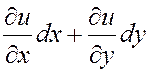.                                    (4.7.1)

О п р е д е л е н и е.  Полным  дифференциалом второго порядка называется полный дифференциал полного дифференциала этой функции: 

.

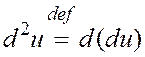      Учитывая (4.7.1), получаем

d().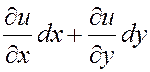

      Эту последнюю формулу надо понимать так, что над выражением, стоящим в скобках, надо произвести действия в соответствии с формулой (4.7.1). Выполняя эти действия, получаем:

+.

.

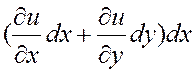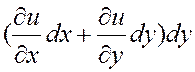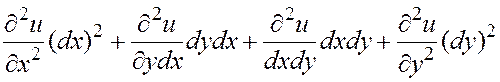      Имея в виду, что производные второго порядка непрерывны, пользуемся равенством смешанных частных производных (теорема п. 4.6):

.

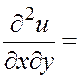
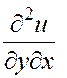Принимаем обозначения:  . Тогда выражение для второго дифференциала принимает вид:

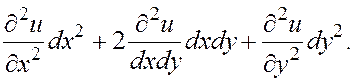              (4.7.2)

      Точно так же определяем полный дифференциал третьего порядка:

.

      При условии непрерывности частных производных третьего порядка он существует и при этом справедлива формула, аналогичная формуле (4.7.2):

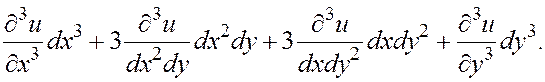  (4.7.3)

      В чем состоит эта аналогия?  При сопоставлении формул (4.7.1),  (4.7.2) и (4.7.3) замечаем, что правая часть напоминает (позволим себе этот неформальный термин) формулу бинома Ньютона соответственно для  n= 1, 2, 3. Эту аналогию мы используем для лаконичной записи символической формулы, выражающей дифференциал любого порядка:

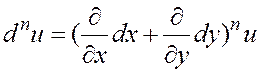,   .                  (4.7.4)

      Таким же образом можно получить соответствующие выражения дифференциалов высших порядков функции трех и более переменных. Продолжая аналогию и применяя символические формулы, введем вектор, который помогает легко запомнить и коротко записать многие формулы дифференциального исчисления функции нескольких переменных.