Дифференцируемость функции. Частное приращение, частный дифференциал и частная производная, страница 3

Если  – независимые переменные, то, как мы видели [1], [5], можно положить    . Поэтому формулу для полного дифференциала (4.4.7) можно записать в такой форме:

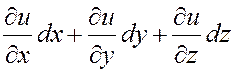.                                  (4.4.9)

      Аналогичная формула имеет место для полного дифференциала числовой функции произвольного числа  независимых переменных :

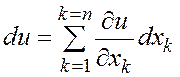.                                  (4.4.10)

      Напомним, что формула (4.4.10) и ее частный случай (4.4.9) справедливы, если  x₁, x₂, . . . ,  x_n  – независимые переменные. Как и для функции одного аргумента [1], [2], [5], эта форма записи дифференциала сохраняется и в том случае, когда, в свою очередь, x₁, x₂, . . . ,  x_n – функции одной или нескольких переменных других переменных. Это свойство дифференциала, состоящее в сохраняемости формы (4.4.10) его записи, называется инвариантностью формы дифференциала. Несложное доказательство инвариантности формы дифференциала, основанное на правиле дифференцирования сложной функции, которое мы определим ниже в п. 4.8, предлагаем провести самостоятельно в качестве полезного упражнения.

     Из формул (4.3.6) следует правило вычисления частных производных числовой функции нескольких переменных:

для того чтобы найти частную производную от функции нескольких переменных по одной из переменных надо найти производную функции этой одной переменой, предполагая, что все остальные переменные сохраняют постоянное значение.

      Так, например, вычисляя ,  полагаем   и дифференцируем  функцию одного аргумента x, считаяyиzпостоянными.

      П р и м е р ы.

1.  . Находим частные производные в произвольной точке :

               ,   ,    

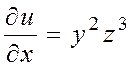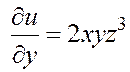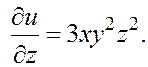
2. 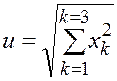   .  В соответствии с правилами дифференцирования получаем частную производную по каждой   переменной x_k:

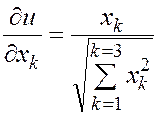,    k= 1, 2, 3.

3.   Вычислим частный дифференциал d_yu  функции  по аргументу y в точке (1, 1), соответствующий приращению .

d_yu  =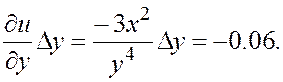   

4.  Вычислим полное приращение и полный дифференциал функции

     в точке (0, 0, 0) для приращений аргументов

                           Dx = 0,02,  Dy=0,01,   Dz = –0, 01.

 Полное приращение:

 

–  =  =

= 0,02956.

    Полный дифференциал:

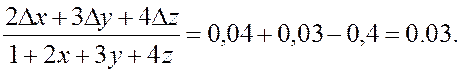
4.5. Дифференцируемость функции общего вида

      Вернемся теперь к рассмотрению функции , которую мы определили в п. 2.1. Здесь  , где m и n – произвольные натуральные числа. В определении дифференцируемости функции (п.4.1) матрица  Аразмераmxn – матрица-производная, строки которой образуют матрицы-производные ее координатных функций :

.

А = = .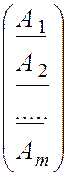

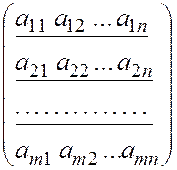       Как мы видели, элементами матрицы-производной каждой координатной функции являются соответствующие частные производные по координатам:

,  .

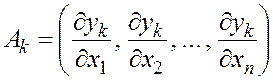      Теперь мы выяснили, что матрицу А образуют частные производные от координатных функций по всем переменным, записанные в определенном порядке:

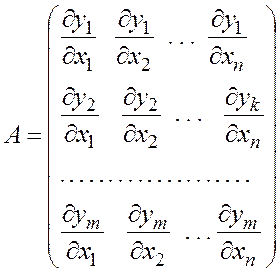
      Эта матрица называется матрицей Якоби.  Определитель квадратной матрицы Якоби (случай, когда ) называется  якобианом.

     П р и м е р ы.

1.  Вычисляем якобиан перехода от декартовых координат на плоскости к полярным. Формулы перехода известны:

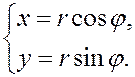
          Находим   частные  производные:

                   .

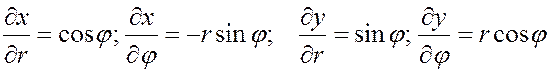           Вычисляем якобиан:

                                       

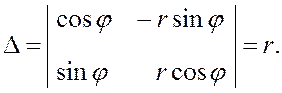
2.  Вычисляем якобиан перехода от декартовых координат в пространстве  к цилиндрическим . Формулы перехода от декартовых координат к цилиндрическим известны:

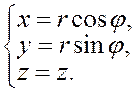
          Находим частные производные, получаем якобиан: .

3.  Вычисляем якобиан перехода от декартовых координат в про-  странстве  к сферическим . Формулы перехода, выражающие  декартовы координаты через сферические:

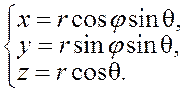
       Подставляя частные производные в якобиан, получаем:

      Результаты, полученные в примерах 1, 2, 3, приведены в следующей таблице. Их следует запомнить.

Старые координаты	Новые координаты	Якобиан
Декартовы	Полярные
Декартовы	Цилиндрические
Декартовы	Сферические