Разработка контента курса дистанционного обучения "DB2 универсальная база данных", страница 29

D(2,3) = 0,15 (0,05+0,15) + 0,7*0,15 = 0,135

D(4,3) = 0,15 (0,05+0,15) + 0,7*0,15 = 0,135

D(5,2) = 0,15 (0,05+0,05) + 0,7*0,15 = 0,12

D(6,7) = 0,15 (0,05+0,15) + 0,7*0,15 = 0,135

D(7,3) = 0,15 (0,15+0,15) + 0,7*0,15 = 0,15

D(7,8) = 0,15 (0,15+0,05) + 0,7*0,05 = 0,065

D(2,1) = 0,15 (0,05+0,05) + 0,7*0,15 = 0,12

D(3,2) = 0,15 (0,05+0,15) + 0,7*0,15 = 0,135

D(3,4) = 0,15 (0,05+0,15) + 0,7*0,05 = 0,065

D(2,5) = 0,15 (0,05+0,05) + 0,7*0,15 = 0,12

D(7,6) = 0,15 (0,05+0,15) + 0,7*0,15 = 0,135

D(3,7) = 0,15 (0,15+0,15) + 0,7*0,15 = 0,15

D(8,7) = 0,15 (0,15+0,05) + 0,7*0,15 = 0,135

Полученная матрица зависимостей первого порядка между всеми парами модулей выглядит так:

Таблица 3.13. Матрица зависимостей между модулями

Проанализируем полученные значения.

Произведем грубую оценку сложности модульной структуры. Для этого суммируем все элементы матрицы и разделим полученную сумму на количество модулей:

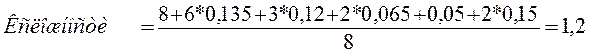
Оценим количество модулей,  которые придется при изменении 1-го модуля структуры. Для этого следует суммировать все элементы i-й строки:

Таблица 3.14. Количество модулей,  которые придется изменить

Нормировочный коэффициент:

К = 42 / 8-1 = 6

Рассчитаем максимальное и минимальное значения для коэффициента сложности и нормировочного коэффициента модульной структуры, чтобы определить насколько значения коэффициентов модульной структуры уровней знаний близки к наилучшим.

Минимальное значение коэффициента сложности рассчитаем из условия, что все модули не связаны, то есть все коэффициенты матрицы, кроме диагональных, равны нулю:

Ксл min = 13/13 = 10/10 = 8/8 = 1

        Из этого же условия найдем максимальное значение нормировочного коэффициента:

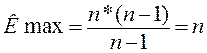                                                                                 (3.3)

Следовательно, из этой формулы найдем: Кmax1= n = 13;

                                                                             К max2 = 10;

                                                                             К max3 = 8.

Максимальное значение коэффициента сложности модульной структуры рассчитаем из условия, что все модули связаны суммой всех связей и прочности модулей так же определяются суммой всех классов прочности:

D = 0,15* (1+1) + 0,7*1 = 1;

Ксл мах1 = (13*12*1 + 13) / 13 = (156 + 13) / 13 = 196 / 13 = 13

Ксл мах2 = (10*9*1 + 10) / 10 = (90 + 10) / 10 = 100 / 10 = 10

Ксл мах3 = (8*7*1 + 8) / 8 = (56 + 8) / 8 = 64 / 8 = 8

Из этого же условия найдем минимальное значение нормировочного коэффициента:

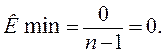                                                                                        (3.4)

Для удобства сравнения, сведем полученные данные в одну таблицу: