Разработка контента курса дистанционного обучения "DB2 универсальная база данных", страница 28

Полученная матрица зависимостей первого порядка между всеми парами модулей выглядит так:

Таблица 3.9. Матрица зависимостей между модулями

Проанализируем полученные значения.

Произведем грубую оценку сложности модульной структуры. Для этого суммируем все элементы матрицы и разделим полученную сумму на количество модулей:

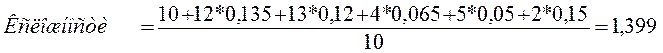
Оценим количество модулей, которые придется при изменении 1-го модуля структуры. Для этого следует суммировать все элементы i-й строки:

Таблица 3.10 Количество модулей, которые придется изменить

Название модуля	Количество модулей, подлежащих изменению
Исполнение приложения	1,375
Среда разработки	1,36
Платформа Java	1,15
Сервлет	1,68
Jsp страница	1,68
JDBC	1,135
Соединение с БД	1,62
Хранимая процедура	1,135
Технология EJB	1,375
Использование EJB	1,48

Рассчитаем нормировочный коэффициент:

К = 54/ 10-1 = 6

3. Высокий уровень знаний обучающихся

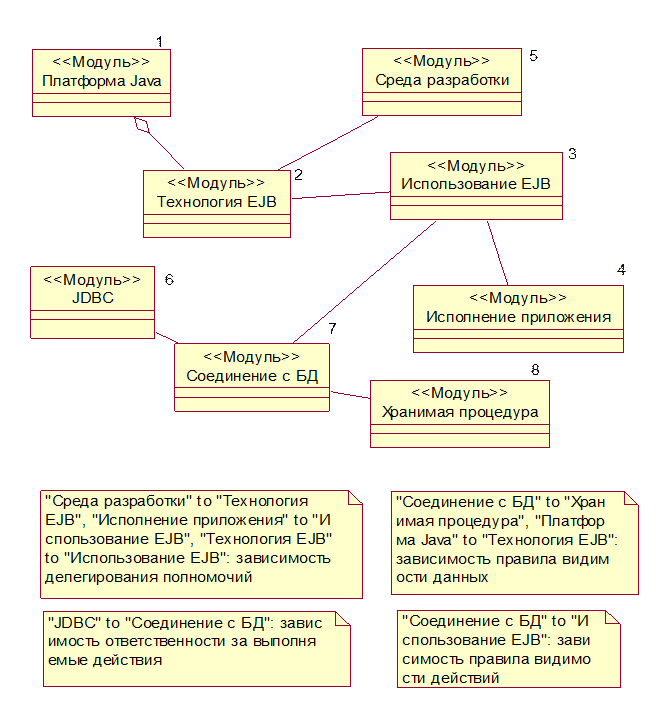
Рис. 3.7 Модульная структура высокого уровня знаний обучающихся

Рассмотрим спецификации модули курса для обучающихся с низким уровнем знаний:

Таблица 3.11. Классы прочности модулей

Таблица 3.12. Виды сцепления модулей

По этим коэффициентам рассчитаем значения матрицы зависимостей:

D(1,2) = 0,15 (0,05+0,05) + 0,7*0,05 = 0,05