Влияние вязкости откачиваемой жидкости и газа на рабочую характеристику насоса. Способы защиты погружного насоса от попадания в него свободного газа, страница 8

Подставив (21) в (20), получим окончательное выражение для коэффициента наполнения насоса с учетом сепарации газа:

                                 η_нап = 1- (1 + m)(1 - К_ес)β_гвх/(1-К_есβ_гвх)                               (23)

где Р_гвх— расходная доля свободного газа в газожидкостной смеси у входа в насос при р_вх и Т_вх.

Анализ формулы (23) показывает степень и характер влия­ния различных факторов на коэффициент наполнения насоса: он снижается при увеличении объема вредного пространства в насо­се и величины расходного газосодержания газожидкостной смеси у входа в насос и, напротив, увеличивается при повышении коэф­фициента сепарации газа.

6.1.2.   КОЭФФИЦИЕНТ  ДЛИНЫ  ХОДА   ПЛУНЖЕРА   НАСОСА

Упругие деформации колонны штанг и подъемных труб, вызван­ные периодическим характером гидростатических сил, инерционных и сил трения, действующих на штанги и НКТ, приводят к умень­шению длины хода плунжера по сравнению с длиной хода головки балансира, то есть S_пл<S_гб. Отношение длины хода плунжера к длине хода головки балансира есть коэффициент длины хода плун­жера:

                                                                          η_ход = S_пл/S_гб.                                            (24)

При определении η_ход основной задачей является определение длины хода плунжера, поскольку длина хода головки балансира всегда известна.

Длина хода плунжера в случае пренебрежимо малых инерци­онных нагрузок с учетом упругих деформаций штанг и труб может быть определена по уравнению:

                                                   S_пл = S_гб – λ_ш – λ_т                                               (25)       

где λ_ш, λ_т — величины упругих деформаций колонны штанг и подъемных труб соответственно. Их значения можно определить, пользуясь законом Гука: деформация прямо пропорциональна на­пряжению, длине стержня и обратно пропорциональна модулю Юнга материала, из которого сделан стержень.

Если принять, что значение растягивающей гидростатической силы соответствует выражению

                                              Т_ст = (Р_вых — Р_вх)πd²_пл/4,                                        (26)

то величина упругих деформаций колонны штанг определяется как

                                                   λ_ш = T_cтL_ш/(f_шE_ш),                                                      (27)

а величина упругих деформаций колонны труб соответственно —

                                                               λ_Т= Т_CTL_T/(f_TЕ_T),

где L_ш, L_т f_ш f_т — длина и площадь сечения колонны штанг и труб соответственно; Е_ш, Е_т — модули упругости материала штанг и труб.

Учитывая, что L_ш ≈L_T, а Е_ш ≈ Е_т, окончательно получим:

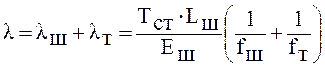                                  .                             (28)

Представляет интерес рассмотреть влияние инерционных сил па величину хода плунжера насоса.

Сила инерции колонны штанг в конце хода вниз направлена вниз и приводит к дополнительному пробегу плунжера после оста­новки головки балансира. То же происходит при ходе колонны штанг вверх: головка балансира уже остановилась, а плунжер вместе с колонной штанг движется по инерции еще некоторое вре­мя вверх.

Дополнительный инерционный пробег плунжера насоса увели­чивает действительный ход плунжера па некоторую величину. Су­ществует много попыток рассчитать дополнительную длину про­бега плунжера.

Приведем здесь формулу Л. С. Лейбензона[2], одну из наиболее простых, но по точности не уступающей другим, более поздним и более громоздким формулам:

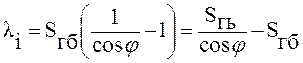                               ,                               (29)

где φ — критерий Коши.

Таким образом, действительная длина хода плунжера штанго­вого глубинного насоса с учетом инерционных сил и упругих   деформаций колонны штанг и подъемных труб определяется выра­жением:

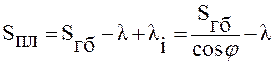                                 ,                                 (30)

а коэффициент длины хода плунжера соответственно —